Hình bình hành là một loại hình học có đặc điểm riêng. Để nhận biết hình bình hành, có một số dấu hiệu quan trọng cần lưu ý. Để giúp bạn hiểu rõ hơn về vấn đề này, dưới đây là bài viết của Hoc2K mang đến những thông tin hữu ích. Mời bạn đọc tham khảo.
Hình bình hành là gì?
Trong hình học Euclid, hình bình hành là một dạng hình tứ giác được hình thành bởi hai cặp đường thẳng song song cắt nhau. Nó có sự tương đồng với hình thang và hình chữ nhật, gồm tổng cộng 4 góc và có những tính chất đặc biệt.
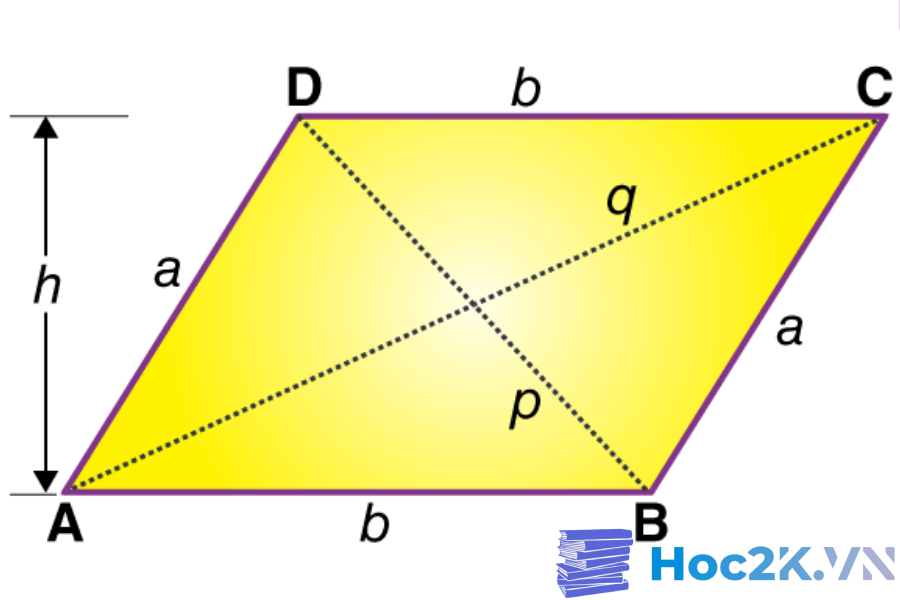
Tính chất hình bình hành
Dấu hiệu nhận biết hình bình hành
Công thức tính chu vi hình bình hành
Chu vi của một hình bình hành bằng gấp đôi tổng độ dài hai cạnh kề nhau bất kỳ:
P = (a + b) x 2
a, b: Độ dài của 2 cạnh bất kỳ của hình bình hành
Công thức tính diện tích hình bình hành
S = a x h
a: Cạnh đáy hình bình hành
h: Chiều cao của hình bình hành
Kết luận
Trên đây là một bài viết giới thiệu về Hình bình hành là gì? Dấu hiệu nhận biết và công thức tính được Hoc2K chia sẻ nhằm mang tính chất tham khảo cho bạn đọc.
Một số câu hỏi thường gặp về hình bình hành
Hình bình hành có 1 góc vuông là hình gì?
Hình bình hành có 1 góc vuông là Hình chữ nhật
Hình bình hành có phải là hình chữ nhật không?
Không, hình bình hành không phải là hình chữ nhật. Mặc dù hình bình hành và hình chữ nhật đều là các dạng hình tứ giác, nhưng chúng có các đặc điểm khác nhau. Trái với hình chữ nhật có các góc vuông, hình bình hành không có góc vuông và có các cạnh song song và bằng nhau. Mặc dù một hình bình hành có thể có dạng tương tự với một hình chữ nhật nếu các cạnh của nó có góc vuông, nhưng không phải tất cả các hình bình hành đều là hình chữ nhật.
Hình bình hành tiếng anh là gì?
Hình bình hành tiếng anh là Parallelogram
