Hình hộp chữ nhật là một khối hình học quen thuộc trong chương trình Toán học từ lớp 5 đến THCS, đồng thời xuất hiện phổ biến trong đời sống dưới dạng hộp carton, bể nước, phòng ở, container vận chuyển hay tủ quần áo. Khối này có sáu mặt đều là hình chữ nhật, giúp dễ dàng mô hình hóa các vật thể thực tế để tính toán thể tích hay diện tích.
Nắm vững tính chất, dấu hiệu nhận biết cùng các công thức liên quan giúp học sinh giải quyết nhanh chóng các bài toán hình không gian ở cấp THCS, từ tính thể tích đến chứng minh dấu hiệu. Đồng thời, kiến thức này mang lại lợi ích thực tiễn lớn trong xây dựng (tính khối lượng bê tông phòng), thiết kế nội thất (ước lượng không gian tủ kệ) và đóng gói logistics (tối ưu thể tích thùng hàng).
Trong bài viết này Hoc2K sẽ hướng dẫn chi tiết từ định nghĩa đến bài tập thực hành về hình hộp chữ nhật giúp bạn áp dụng hiệu quả cả trong học tập lẫn công việc.
Định nghĩa hình hộp chữ nhật và các yếu tố cơ bản
Hình hộp chữ nhật là khối đa diện có sáu mặt, trong đó tất cả các mặt đều là hình chữ nhật. Mỗi cặp mặt đối song song và bằng nhau. Các yếu tố cơ bản của hình hộp chữ nhật:
- Có 6 mặt (trước – sau, trên – dưới, trái – phải) đều là hình chữ nhật.
- Có 12 cạnh, chia thành 3 nhóm cạnh song song, bằng nhau.
- Có 8 đỉnh, nơi gặp nhau của ba cạnh.
- Có 3 kích thước đặc trưng gồm chiều dài, chiều rộng và chiều cao, thường ký hiệu là (a hoặc d, b hoặc r, c hoặc h).
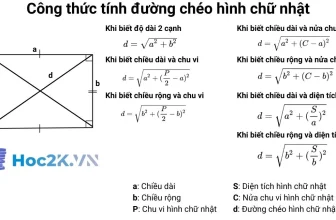
- Có đường chéo là đoạn thẳng nối hai đỉnh đối nhau trong không gian với độ dài là
Đặc điểm nhận biết hình hộp chữ nhật
Một vật thể được coi là hình hộp chữ nhật khi:
- Có 6 mặt đều là hình chữ nhật.
- Các mặt đối song song và bằng nhau.
- Các cạnh bên song song, bằng nhau và vuông góc với mặt đáy.
Nhờ những đặc điểm này, hình hộp chữ nhật thường được dùng trong xây dựng, thiết kế nội thất và sản xuất bao bì vì dễ tính toán thể tích, diện tích và bố trí không gian.
Các công thức liên quan đến hình hộp chữ nhật
Hình hộp chữ nhật có nhiều đại lượng hình học liên quan với nhau như thể tích, diện tích, và độ dài các đường chéo. Việc nắm được các công thức cơ bản giúp ta dễ dàng tính toán trong học tập và ứng dụng thực tế như đo lường, thiết kế hay lập kế hoạch xây dựng.
Công thức tính thể tích hình hộp chữ nhật
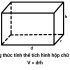
Cách tính thể tích hình hộp chữ nhật bằng tích của chiều dài, chiều rộng và chiều cao hoặc diện tích mặt đáy nhân với chiều cao.
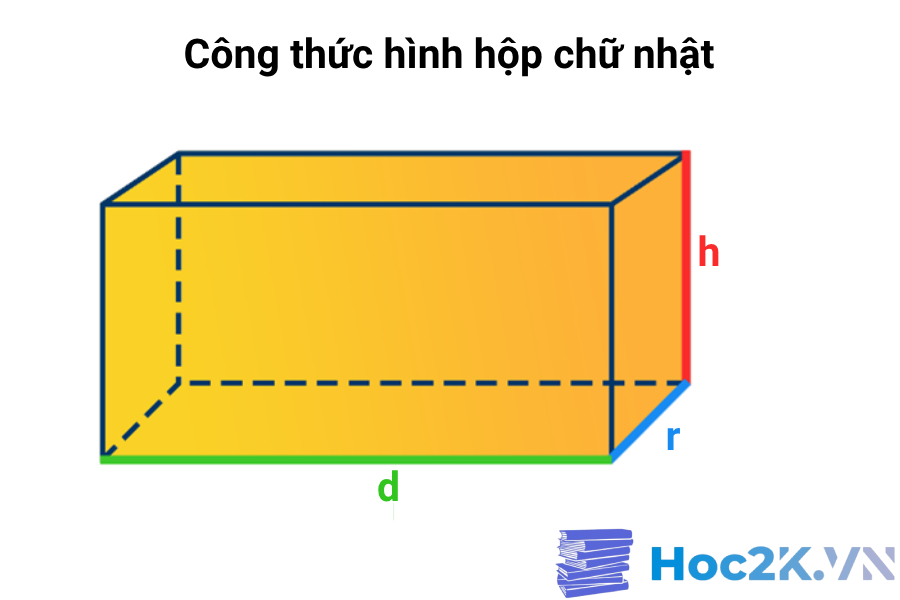
Cách tính thể tích hình hộp chữ nhật: V = d x r x h hoặc V = Sđáy x h
Trong đó:
- d: Chiều dài mặt đáy
- r: Chiều rộng mặt đáy
- h: Chiều cao
- Sđáy: Diện tích mặt đáy
- V: Thể tích
Thể tích là đặc điểm quan trọng của khối không gian, thể hiện khả năng chiếm dụng trong thực tế. Nó được xác định từ sự kết hợp các chiều đo để tạo nên không gian ba chiều, không chỉ mang ý nghĩa toán học mà còn có nhiều ứng dụng thực tiễn như đo sức chứa thùng hàng hay ước lượng vật liệu trong xây dựng.
Công thức tính chu vi hình hộp chữ nhật
Cách tính chu vi hình hộp chữ nhật bằng bốn nhân với tổng của chiều dài, chiều rộng và chiều cao.
Cách tính chu vi hình hộp chữ nhật: P = 4 x (d + r + h)
Trong đó:
- d: Chiều dài mặt đáy
- r: Chiều rộng mặt đáy
- h: Chiều cao
- P: Tổng độ dài các cạnh.
Công thức chu vi hình hộp chữ nhật giúp xác định tổng chiều dài các cạnh của khối, từ đó hỗ trợ ước lượng vật liệu cần dùng cho khung, viền hoặc hệ kết cấu bao quanh. Trong thực tế, việc tính chu vi cho phép dự đoán chính xác độ dài thanh kim loại, gỗ hoặc dây bao cần thiết, góp phần tối ưu chi phí và hạn chế sai sót trong thi công, đóng gói và thiết kế.
Công thức tính chu vi mặt đáy hình hộp chữ nhật
Cách tính chu vi mặt đáy hình hộp chữ nhật bằng 2 nhân với tổng của chiều dài, chiều rộng mặt đáy.
Cách tính chu vi mặt đáy hình hộp chữ nhật: Pđáy = 2 x (d + r)
Trong đó:
- d: Chiều dài mặt đáy
- r: Chiều rộng mặt đáy
- Pđáy: Chu vi mặt đáy
Công thức chu vi mặt đáy hình hộp chữ nhật được dùng để xác định độ dài đường bao quanh đáy của khối, từ đó phục vụ việc thiết kế và thi công các bộ phận tiếp xúc với mặt nền. Trong thực tế, đại lượng này giúp ước lượng vật liệu làm khung đáy, viền móng, mép thùng hoặc phần tiếp đất của công trình, góp phần tính toán chính xác và tiết kiệm vật liệu.
Công thức tính diện tích xung quanh hình hộp chữ nhật
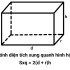
Cách tính diện tích xung quanh hình hộp chữ nhật bằng chu vi đáy nhân với chiều cao hoặc 2 lần tổng chiều dài và chiều rộng sau đó nhân với chiều cao.
Cách tính diện tích xung quanh hình hộp chữ nhật: Sxq = Pđáy x h = 2 x (d + r) x h
Trong đó:
- d: Chiều dài
- r: Chiều rộng
- h: Chiều cao
- Pđáy: Chu vi mặt đáy
- Sxq: Diện tích xung quanh
Công thức diện tích xung quanh hình hộp chữ nhật dùng để tính tổng diện tích của các mặt bên bao quanh khối, phản ánh phần “lớp vỏ” bên ngoài không tính hai mặt đáy. Đại lượng này có ý nghĩa thực tiễn trong việc ước lượng diện tích cần sơn, dán, bọc hoặc phủ vật liệu cho thùng, phòng, bể chứa…, giúp tính toán chính xác khối lượng vật liệu và hạn chế lãng phí.
Công thức tính diện tích toàn phần hình hộp chữ nhật
Cách tính diện tích toàn phần hình hộp chữ nhật bằng tổng diện tích xung quanh và diện tích hai đáy.
Cách tính diện tích toàn phần hình hộp chữ nhật: Stp = Sxq + Sđáy = 2 x ( dr + dh + rh)
Trong đó:
- d: Chiều dài
- r: Chiều rộng
- h: Chiều cao
- Sđáy: Diện tích hai đáy = 2 x (d + r)
- Sxq: Diện tích xung quanh
Công thức diện tích toàn phần hình hộp chữ nhật cho biết tổng diện tích của tất cả các mặt bao quanh khối, bao gồm cả mặt đáy và mặt trên. Đại lượng này được sử dụng khi cần tính diện tích phủ kín toàn bộ bề mặt như sơn, ốp, bọc hoặc cách nhiệt, giúp ước lượng chính xác lượng vật liệu cần thiết trong xây dựng, đóng gói và thiết kế không gian.
Các dạng bài tập về hình hộp chữ nhật
Dạng 1: Tính diện tích toàn phần của hình hộp chữ nhật
Đề bài 1 (cơ bản): Một hình hộp chữ nhật có chiều dài a=8cm, chiều rộng b=5cm, và chiều cao h=10cm. Hãy tính diện tích toàn phần của hình hộp chữ nhật này.
Cách giải tham khảo:
Áp dụng công thức diện tích toàn phần hình hộp chữ nhật: Stp=Sxq+Sđáy=2(a+b)h+ 2ab
Thay số: Stp=Sxq+Sđáy=2x(8+5)x10 + 2x8x5=340cm2
Đề bài 2 (mở rộng): Một hình hộp chữ nhật có chiều dài a=10 cm, chiều rộng b=6 cm và diện tích toàn phần Stp=376 cm2. Tính chiều cao hhh của hình hộp.
Cách giải tham khảo:
Áp dụng công thức diện tích toàn phần hình hộp chữ nhật: Stp=Sxq+Sđáy=2(a+b)h+ 2ab
Thay số: 376=2x(10+6)h+2x10x6 ⇔ 376=32h+120 ⇔ h = 8 cm
Dạng 2: Tính thể tích của hình hộp chữ nhật
Đề bài 1 (cơ bản): Một bể nước hình hộp chữ nhật có chiều dài a=2 m, chiều rộng b=1.5 m và chiều cao h=1 m. Tính thể tích của bể nước này.
Cách giải tham khảo:
Áp dụng công thức thể tích hình hộp chữ nhật: V=abh
Thay số: V=2×1.5×1=3m3
Đề bài 2 (mở rộng): Một hình hộp chữ nhật có thể tích V=540 cm3 và chiều cao h=9 cm. Biết rằng chiều dài a gấp đôi chiều rộng b. Tìm a và b.
Cách giải tham khảo:
Áp dụng công thức thể tích hình hộp chữ nhật: V=abh và tỷ số a=2b
Thay số: 540=2bxbx9 ⇔ 540=18b2 ⇔ b2=30 ⇔ b= √30 và a=2√30
Dạng 3: Tính diện tích xung quanh của hình hộp chữ nhật
Đề bài 1 (cơ bản): Một chiếc hộp quà có chiều dài a=12 cm, chiều rộng b=8 cm và chiều cao h=15 cm. Hãy tính diện tích xung quanh của chiếc hộp này.
Cách giải tham khảo:
Áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật: Sxq=2(a+b)h
Thay số: Sxq=2x(12+8)x15=600 cm2
Khi giải các bài toán về diện tích xung quanh, diện tích toàn phần hoặc thể tích hình hộp chữ nhật, cần thống nhất đơn vị đo. Với bài toán phức tạp, nên vẽ hình và ghi chú các đại lượng để hạn chế sai sót.
Kết luận
Hình hộp chữ nhật, một khái niệm cơ bản trong hình học, đã được áp dụng rộng rãi vào nhiều lĩnh vực khác nhau. Chúng ta đã tìm hiểu về Định nghĩa, Tính chất, Dấu hiệu và các công thức về hình hộp chữ nhật cùng với một số ví dụ và ứng dụng thực tế của hình hộp chữ nhật. Hiểu về hình hộp chữ nhật giúp chúng ta sử dụng nó một cách hiệu quả và áp dụng vào cuộc sống hàng ngày.