Hình hộp chữ nhật là một hình không gian quen thuộc trong đời sống. Nó có ba kích thước chính: chiều dài, chiều rộng và chiều cao. Trong đó, chiều cao đóng vai trò quan trọng. Nó giúp ta biết được độ cao của hình hộp. Chiều cao cũng là yếu tố then chốt để tính thể tích và diện tích. Bài viết này Hoc2K sẽ giúp bạn hiểu rõ về chiều cao hình hộp chữ nhật. Bạn sẽ biết cách tính chiều cao của hình hộp chữ nhật trong nhiều trường hợp khác nhau. Từ đó, bạn có thể áp dụng vào các bài toán thực tế.
Chiều cao hình hộp chữ nhật là gì?
Hình hộp chữ nhật có ba kích thước chính. Đó là chiều dài, chiều rộng và chiều cao. Chiều cao là khoảng cách từ mặt đáy lên mặt trên. Nó giúp ta biết hình hộp cao bao nhiêu. Chiều cao rất quan trọng khi tính thể tích. Nó cũng cần thiết khi tính diện tích xung quanh. Hiểu về chiều cao giúp ta giải quyết nhiều bài toán thực tế.
Định nghĩa chiều cao
Chiều cao của hình hộp chữ nhật là khoảng cách từ mặt dưới lên mặt trên. Nó là một trong ba kích thước chính của hình hộp. Ba kích thước này gồm chiều dài, chiều rộng và chiều cao. Chúng quyết định kích thước của hình hộp. Trong toán học, ta thường dùng chữ h hoặc c để ký hiệu chiều cao. Khi vẽ hình hộp, chiều cao là đường thẳng đứng. Nó đi từ mặt dưới lên mặt trên của hình hộp.
Vị trí của chiều cao trong hình hộp chữ nhật
Vị trí của chiều cao trong hình hộp chữ nhật được xác định tùy thuộc vào cách đặt hình hộp trong không gian ba chiều. Tuy nhiên, theo quy ước thông thường, chiều cao thường được xem là kích thước theo phương thẳng đứng của hình hộp.
Khi xét một hình hộp chữ nhật đặt trên mặt phẳng ngang, chiều cao sẽ là:
- Cạnh vuông góc với mặt phẳng ngang (mặt đáy)
- Khoảng cách ngắn nhất từ mặt đáy đến mặt đối diện (mặt trên)
- Cạnh song song với trục Oz trong hệ tọa độ không gian Oxyz
Trong biểu diễn hình học, chúng ta có thể hình dung vị trí của chiều cao thông qua các yếu tố sau:
Nếu gọi các đỉnh của hình hộp chữ nhật là A, B, C, D (đáy dưới) và A’, B’, C’, D’ (đáy trên), thì chiều cao chính là độ dài của các đoạn thẳng AA’, BB’, CC’ hoặc DD’
Các cạnh này song song với nhau và vuông góc với mặt đáy ABCD
Điều quan trọng cần lưu ý là vị trí của chiều cao có thể thay đổi tùy thuộc vào góc nhìn và cách đặt hình hộp. Trong một số trường hợp, người ta có thể quy ước cạnh nào là chiều cao tùy thuộc vào bài toán cụ thể. Tuy nhiên, một khi đã xác định chiều nào là chiều cao, chúng ta cần nhất quán trong suốt quá trình giải toán để tránh nhầm lẫn.
Đơn vị đo chiều cao
Chiều cao của hình hộp chữ nhật được đo bằng các đơn vị đo độ dài tương tự như các kích thước khác trong hình học. Việc lựa chọn đơn vị đo phù hợp phụ thuộc vào kích thước thực tế của hình hộp và mục đích sử dụng.
Các đơn vị đo phổ biến
Trong hệ mét (SI)
- Milimet (mm): Thường dùng cho các vật thể nhỏ, độ chính xác cao
- Centimet (cm): Phổ biến trong học tập và đo đạc hàng ngày
- Decimet (dm): Đôi khi được sử dụng trong một số bài toán
- Mét (m): Đơn vị cơ bản, thích hợp cho các vật thể lớn như phòng ốc, nhà cửa
- Kilomet (km): Hiếm khi sử dụng cho chiều cao hình hộp, chủ yếu dùng cho khoảng cách lớn
Trong hệ Anh
- Inch (in): Khoảng 2.54 cm, thường dùng trong một số ngành công nghiệp
- Foot (ft): Khoảng 30.48 cm, dùng phổ biến trong kiến trúc
- Yard (yd): Khoảng 91.44 cm
- Mile (mi): Rất hiếm khi sử dụng cho chiều cao hình hộp
Lưu ý về đơn vị đo
Khi tính toán, cần đảm bảo tất cả các kích thước (chiều dài, chiều rộng, chiều cao) đều sử dụng cùng một đơn vị đo để tránh sai sót. Trong các bài toán, đơn vị đo chiều cao nên được ghi rõ ràng trong kết quả
Khi chuyển đổi giữa các đơn vị đo, cần tuân theo quy tắc chuyển đổi chính xác:
- 1 m = 10 dm = 100 cm = 1000 mm
- 1 km = 1000 m
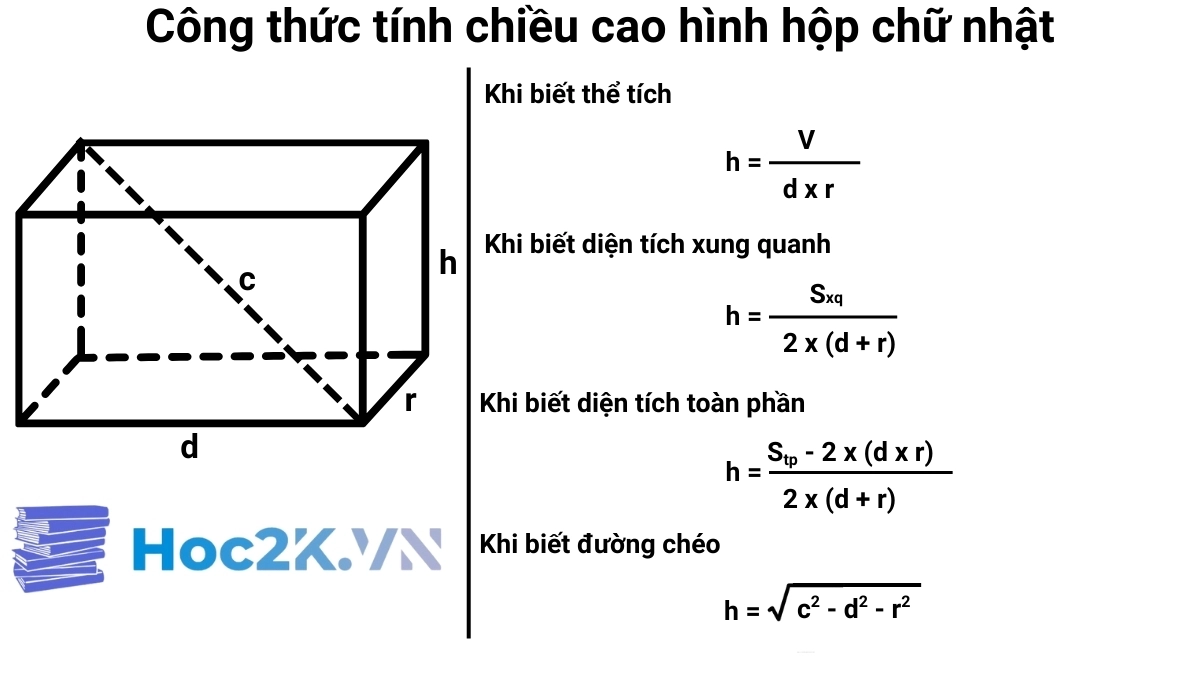
Công thức tính chiều cao hình hộp chữ nhật
Việc tính chiều cao của hình hộp chữ nhật là một kỹ năng quan trọng trong hình học không gian, đặc biệt khi chúng ta cần xác định kích thước đầy đủ của một vật thể. Trong nhiều trường hợp, chiều cao là thông số cuối cùng cần tìm sau khi đã biết các thông số khác như thể tích, diện tích xung quanh, chiều dài và chiều rộng.
Chiều cao của hình hộp chữ nhật có thể được tính toán thông qua nhiều công thức cơ bản, tùy thuộc vào các thông số đã biết. Dưới đây là các công thức quan trọng nhất để xác định chiều cao (h) của hình hộp chữ nhật:
Từ thể tích
![\[h\;=\;\frac V{d\;\times\;r}\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-049ce66c967fb4eac51e380c4c4afa72_l3.png "Rendered by QuickLaTeX.com")
d: Chiều dài hình hộp chữ nhật
r: Chiều rộng hình hộp chữ nhật
h: Chiều cao hình hộp chữ nhật
Từ diện tích xung quanh
![\[h\;=\;\frac{S_{xq}}{2\;\times\;(d\;+\;r)}\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-3cc7da1abcb7690543e2cbfe317556a0_l3.png "Rendered by QuickLaTeX.com")
d: Chiều dài hình hộp chữ nhật
r: Chiều rộng hình hộp chữ nhật
h: Chiều cao hình hộp chữ nhật
Từ diện tích toàn phần
![\[h\;=\;\frac{S_{tp}-\;2\;\times\;(d\;\times\;r)}{2\;\times\;(d\;+\;r)}\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-8c272b18bbe1dff00a4e67dfab852239_l3.png "Rendered by QuickLaTeX.com")
d: Chiều dài hình hộp chữ nhật
r: Chiều rộng hình hộp chữ nhật
h: Chiều cao hình hộp chữ nhật
Từ đường chéo hình hộp
![\[h\;=\;\sqrt{d^2\;-\;a^2\;-\;b^2}\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-d1c9229a232acde033c56565d60be4fe_l3.png "Rendered by QuickLaTeX.com")
a: Chiều dài hình hộp chữ nhật
b: Chiều rộng hình hộp chữ nhật
h: Chiều cao hình hộp chữ nhật
Ví dụ các trường hợp tính chiều cao
Việc tính chiều cao của hình hộp chữ nhật có thể được thực hiện trong nhiều tình huống khác nhau, tùy thuộc vào thông tin đã biết. Mỗi trường hợp đòi hỏi cách tiếp cận riêng và áp dụng các công thức phù hợp để tìm ra kết quả chính xác dưới đây là các ví dụ được áp dụng các công thức tính đường cao hình hộp chữ nhất mà Hoc2K đã đề cập ở trên.
Ví dụ minh họa tính chiều cao khi biết thể tích
Ví dụ: Một hình hộp chữ nhật có thể tích 120 cm³, chiều dài 6 cm và chiều rộng 4 cm. Hãy tính chiều cao của hình hộp chữ nhật này.
Giải:
- Thể tích V = 120 cm³
- Chiều dài a = 6 cm
- Chiều rộng b = 4 cm
- Áp dụng công thức: h = V / (a × b)
- Thay số: h = 120 / (6 × 4) = 120 / 24 = 5 cm
Vậy chiều cao của hình hộp chữ nhật là 5 cm.
Ví dụ minh họa tính chiều cao khi biết chiều dài và chiều rộng
Ví dụ: Một hình hộp chữ nhật có chiều dài 8 cm và chiều rộng 5 cm. Biết rằng diện tích toàn phần của hình hộp là 236 cm². Hãy tính chiều cao của hình hộp.
Giải:
- Chiều dài a = 8 cm
- Chiều rộng b = 5 cm
- Diện tích toàn phần S = 236 cm²
- Diện tích toàn phần được tính theo công thức: S = 2(a × b + a × h + b × h)
- Thay số: 236 = 2(8 × 5 + 8 × h + 5 × h) = 2(40 + 8h + 5h) = 2(40 + 13h) = 80 + 26h
- Vậy: 236 = 80 + 26h
- Suy ra: 26h = 236 – 80 = 156
- Do đó: h = 156 ÷ 26 = 6 cm
Vậy chiều cao của hình hộp chữ nhật là 6 cm.
Ví dụ minh họa tính chiều cao khi biết diện tích xung quanh
Ví dụ: Một hình hộp chữ nhật có chiều dài 10 cm và chiều rộng 6 cm. Diện tích xung quanh của hình hộp là 128 cm². Tính chiều cao của hình hộp chữ nhật.
Giải:
- Chiều dài a = 10 cm
- Chiều rộng b = 6 cm
- Diện tích xung quanh Sxq = 128 cm²
- Áp dụng công thức: Sxq = 2h × (a + b)
- Thay số: 128 = 2h × (10 + 6) = 2h × 16 = 32h
- Suy ra: h = 128 ÷ 32 = 4 cm
Vậy chiều cao của hình hộp chữ nhật là 4 cm.
Ví dụ minh họa tính chiều cao khi biết diện tích toàn phần
Ví dụ: Một hình hộp chữ nhật có chiều dài 8 cm và chiều rộng 5 cm. Diện tích toàn phần của hình hộp là 236 cm². Tính chiều cao của hình hộp chữ nhật.
Giải:
- Chiều dài a = 8 cm
- Chiều rộng b = 5 cm
- Diện tích toàn phần S = 236 cm²
- Áp dụng công thức: S = 2(ab + ah + bh)
- Thay số: 236 = 2(8×5 + 8×h + 5×h) = 2(40 + 8h + 5h) = 2(40 + 13h) = 80 + 26h
- Suy ra: 236 = 80 + 26h
- Do đó: 26h = 236 – 80 = 156
- Vậy: h = 156 ÷ 26 = 6 cm
Vậy chiều cao của hình hộp chữ nhật là 6 cm.
Bài tập ứng dụng từ cơ bản đến nâng cao
Bạn đã học các công thức tính chiều cao hình hộp chữ nhật. Bạn cũng đã xem các ví dụ minh họa. Bây giờ là lúc làm bài tập. Bài tập giúp bạn nhớ công thức tốt hơn. Nó cũng giúp bạn biết cách dùng công thức trong nhiều trường hợp khác nhau. Khi làm bài tập, bạn sẽ rèn luyện tư duy logic. Bạn cũng sẽ học cách phân tích bài toán. Đây là cách tốt để nắm vững kiến thức.
Bài tập tính chiều cao cơ bản
Dưới đây là 10 bài tập cơ bản giúp bạn luyện tập kỹ năng tính chiều cao hình hộp chữ nhật:
- Bài tập 1: Tính chiều cao của hình hộp chữ nhật có thể tích 300 cm³, chiều dài 10 cm và chiều rộng 6 cm.
- Bài tập 2: Một hình hộp chữ nhật có diện tích xung quanh là 280 cm². Biết chiều dài là 12 cm và chiều rộng là 8 cm. Tính chiều cao của hình hộp chữ nhật.
- Bài tập 3: Một hình hộp chữ nhật có diện tích toàn phần là 448 cm². Biết chiều dài là 14 cm và chiều rộng là 8 cm. Tính chiều cao của hình hộp chữ nhật.
- Bài tập 4: Một hộp đựng quà có dạng hình hộp chữ nhật với chiều dài 18 cm và chiều rộng 12 cm. Nếu thể tích của hộp quà là 1.296 cm³, hãy tính chiều cao của hộp.
- Bài tập 5: Một hình hộp chữ nhật có chiều dài 15 cm, chiều rộng 9 cm. Biết diện tích xung quanh của hình hộp là 264 cm². Tính chiều cao của hình hộp.
- Bài tập 6: Một hình hộp chữ nhật có diện tích toàn phần là 292 cm². Biết chiều dài là 9 cm và chiều rộng là 5 cm. Tính chiều cao của hình hộp chữ nhật.
- Bài tập 7: Một hình hộp chữ nhật có thể tích 750 cm³. Biết chiều dài và chiều rộng tỉ lệ 5:3 và chiều dài là 15 cm. Tính chiều cao của hình hộp.
- Bài tập 8: Một hộp đựng đồ có dạng hình hộp chữ nhật với chiều dài 16 cm và chiều rộng 10 cm. Nếu diện tích mặt bên của hộp là 312 cm², hãy tính chiều cao của hộp.
- Bài tập 9: Một hình hộp chữ nhật có thể tích 180 cm³ và diện tích toàn phần là 222 cm². Biết chiều dài là 6 cm và chiều rộng là 5 cm. Tính chiều cao của hình hộp và kiểm tra lại kết quả.
- Bài tập 10: Một hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 15 cm. Biết rằng diện tích mặt đáy cộng với diện tích xung quanh bằng 950 cm². Tính chiều cao của hình hộp chữ nhật.
Bài tập tính chiều cao nâng cao
Dưới đây là 10 bài tập nâng cao giúp bạn thử nâng cao kỹ năng tính chiều cao hình hộp chữ nhật:
- Bài tập 1: Một hình hộp chữ nhật có tổng chiều dài, chiều rộng và chiều cao là 30 cm. Biết thể tích của hình hộp là 405 cm³ và diện tích xung quanh là 183 cm². Tính chiều cao của hình hộp chữ nhật.
- Bài tập 2: Một hình hộp chữ nhật có diện tích toàn phần là 1.460 cm². Biết chiều dài là 30 cm, chiều rộng là 20 cm và chiều cao là x cm. Tính giá trị của x, biết rằng tổng thể tích và diện tích đáy của hình hộp là một số nguyên.
- Bài tập 3: Một thùng chứa nước hình hộp chữ nhật có đáy là hình vuông cạnh a cm. Biết diện tích toàn phần của thùng là 1.200 cm² và thể tích là 2.000 cm³. Tính chiều cao của thùng.
- Bài tập 4: Một hình hộp chữ nhật có tỉ lệ giữa chiều dài, chiều rộng và chiều cao là 5:3:2. Biết diện tích toàn phần của hình hộp là 1.420 cm². Tính chiều cao của hình hộp.
- Bài tập 5: Một hình hộp chữ nhật có thể tích 1.728 cm³. Biết diện tích xung quanh của hình hộp gấp 3 lần tổng diện tích hai mặt đáy, và chiều dài gấp đôi chiều rộng. Tính chiều cao của hình hộp.
- Bài tập 6: Một thùng đựng hàng hình hộp chữ nhật với đáy là hình vuông cạnh 0,8 m. Thùng được làm từ một loại gỗ có giá 120.000 đồng/m². Biết chi phí làm thùng (không tính nắp) là 432.000 đồng. Tính chiều cao của thùng.
- Bài tập 7: Một bể chứa nước hình hộp chữ nhật có thể tích 7,2 m³. Biết chiều dài của bể là 3 m, gấp đôi chiều rộng. Nếu người ta tăng chiều cao thêm 0,5 m và giảm chiều rộng đi 0,2 m (giữ nguyên chiều dài) thì thể tích sẽ tăng thêm 1,5 m³. Tính chiều cao ban đầu của bể.
- Bài tập 8: Một hình hộp chữ nhật có chiều dài 12 cm và chiều rộng 9 cm. Người ta tăng chiều cao ban đầu thêm 2 cm và thấy rằng diện tích toàn phần tăng thêm 126 cm². Tính chiều cao ban đầu của hình hộp.
- Bài tập 9: Một hình hộp chữ nhật có diện tích xung quanh là 480 cm². Biết tỉ lệ giữa chiều dài, chiều rộng và chiều cao là 3:2:4, và thể tích của hình hộp là bội số của 100 cm³. Tính chiều cao của hình hộp chữ nhật.
- Bài tập 10: Một hộp quà hình hộp chữ nhật có đáy là hình chữ nhật với chiều dài 25 cm và chiều rộng 20 cm. Hộp quà được làm từ một tấm bìa cứng hình chữ nhật có chiều dài 85 cm và chiều rộng 60 cm (tấm bìa này được gấp lại để tạo thành hộp quà, không có mối nối). Tính chiều cao tối đa có thể của hộp quà.
Bài tập áp dụng thực tế
Dưới đây là các bài tập thực tế giúp bạn áp dụng kiến thức về tính chiều cao hình hộp chữ nhật vào các tình huống trong đời sống:
- Bài tập 1: Một gia đình cần xây một bể chứa nước hình hộp chữ nhật có đáy là 2,5m × 1,8m. Họ cần bể chứa được 9.000 lít nước. Hãy tính chiều cao tối thiểu cần xây cho bể nước. (Biết 1m³ = 1.000 lít)
- Bài tập 2: Một nhà sản xuất cần thiết kế một hộp đựng bánh có đáy hình chữ nhật kích thước 30cm × 25cm. Hộp được làm từ một loại giấy đặc biệt với diện tích bề mặt tổng cộng là 3.350cm². Hãy tính chiều cao của hộp bánh.
- Bài tập 3: Một lớp học có hình dạng hình hộp chữ nhật với chiều dài 8m và chiều rộng 6m. Theo quy định về thông gió và không gian, mỗi học sinh cần có ít nhất 4m³ không khí. Nếu lớp học có 35 học sinh, hãy tính chiều cao tối thiểu của lớp học.
- Bài tập 4: Một khu bể bơi mini trong nhà có dạng hình hộp chữ nhật kích thước 4m × 2,5m. Chi phí để làm phần tường xung quanh bể (không tính đáy) là 4.200.000 đồng với đơn giá 350.000 đồng/m². Hãy tính chiều sâu của bể bơi.
- Bài tập 5: Một công ty đóng gói cần thiết kế hộp carton hình hộp chữ nhật có đáy 40cm × 30cm để đựng sản phẩm. Mỗi hộp carton cần sử dụng 0,56m² vật liệu (bao gồm cả phần đáy và nắp). Tính chiều cao của hộp.
- Bài tập 6: Một phòng kho hình hộp chữ nhật có chiều dài 5m và chiều rộng 4m. Người quản lý cần đặt 80 thùng hàng (mỗi thùng có thể tích 0,125m³) vào kho sao cho chiều cao xếp chồng không quá 2m. Tính chiều cao tối thiểu của phòng kho để đảm bảo có đủ không gian cho hệ thống chiếu sáng và thông gió phía trên.
- Bài tập 7: Một hồ cá cảnh hình hộp chữ nhật có đáy 80cm × 40cm. Biết rằng lượng nước trong hồ là 112 lít và mực nước cách miệng hồ 5cm. Tính chiều cao của hồ cá. (Biết 1 lít = 1.000cm³)
- Bài tập 8: Một nhà thiết kế cần làm một chiếc hộp đựng trang sức hình hộp chữ nhật có đáy hình vuông cạnh 12cm. Họ có một tấm gỗ quý diện tích 576cm² để làm tất cả các mặt của hộp (bao gồm cả đáy và nắp). Tính chiều cao tối đa có thể của chiếc hộp.
- Bài tập 9: Một công ty sản xuất thùng rác từ nhựa tái chế. Mỗi thùng có đáy hình chữ nhật 35cm × 25cm và chiều cao h cm. Biết rằng mỗi thùng tiêu thụ 0,5kg nhựa và định mức tiêu thụ nhựa là 0,4kg/m² bề mặt. Tính chiều cao h của thùng rác.
- Bài tập 10: Một nhà hàng cần đặt làm một bể nuôi hải sản hình hộp chữ nhật có đáy 1,5m × 1,2m. Chi phí làm bể là 6.300.000 đồng, trong đó chi phí làm đáy là 1.800.000 đồng và chi phí làm mỗi m² mặt bên là 700.000 đồng. Tính chiều cao của bể.
- Bài tập 11: Một phòng học có dạng hình hộp chữ nhật với chiều dài 12m và chiều rộng 8m. Theo quy định về âm học, tỉ lệ giữa thể tích phòng và diện tích bề mặt phải nằm trong khoảng từ 1,5 đến 1,8. Tính khoảng giá trị chiều cao phù hợp của phòng học.
- Bài tập 12: Một hộp đựng bưu kiện có dạng hình hộp chữ nhật với chiều dài 50cm và chiều rộng 30cm. Theo quy định của dịch vụ chuyển phát, tổng ba kích thước (dài + rộng + cao) không được vượt quá 150cm và thể tích không quá 60.000cm³. Tính chiều cao tối đa có thể của kiện hàng.
Bài tập áp dụng thực tế tính chiều cao bể nước
- Bài tập 1: Một gia đình cần xây một bể chứa nước hình hộp chữ nhật có đáy là 2m × 1,5m. Họ cần bể chứa được 6.000 lít nước. Hãy tính chiều cao tối thiểu cần xây cho bể nước. (Biết 1m³ = 1.000 lít)
- Bài tập 2: Một công ty xây dựng cần thiết kế một bể chứa nước ngầm cho một tòa nhà văn phòng. Bể có đáy hình chữ nhật với kích thước 4m × 3m. Diện tích các mặt bên (tường bể) là 42m². Tính chiều cao của bể và thể tích nước mà bể có thể chứa.
- Bài tập 3: Một khu chung cư cần xây một bể chứa nước dự phòng hình hộp chữ nhật. Do hạn chế về diện tích, họ chỉ có thể xây bể với đáy có kích thước 5m × 4m. Theo quy định, mỗi hộ gia đình (có 40 hộ) cần được cung cấp ít nhất 500 lít nước dự phòng. Tính chiều cao tối thiểu của bể nước.
- Bài tập 4: Một nông trại cần xây một bể chứa nước tưới cây hình hộp chữ nhật có đáy 6m × 5m. Chi phí xây dựng các mặt bên của bể là 12.600.000 đồng với đơn giá 300.000 đồng/m². Tính chiều cao của bể và thể tích nước mà bể có thể chứa.
- Bài tập 5: Một nhà máy cần xây một bể nước xử lý hình hộp chữ nhật có đáy 8m × 6m. Biết rằng tổng diện tích bề mặt (bao gồm cả đáy và mặt trên) của bể là 296m². Tính chiều cao của bể và thể tích nước mà bể có thể chứa.
- Bài tập 6: Một trường học cần xây một bể nước dự trữ hình hộp chữ nhật. Bể có đáy hình vuông cạnh 4m và chiều cao h m. Nếu thể tích của bể là 80m³ và chi phí xây dựng tường bể (các mặt bên) là 64 triệu đồng (đơn giá 800.000 đồng/m²), hãy kiểm tra xem chiều cao h có phù hợp với các số liệu trên không?
- Bài tập 7: Một khu biệt thự cần thiết kế một bể bơi có đáy hình chữ nhật kích thước 12m × 8m. Biết rằng thể tích nước trong bể là 336m³ và mực nước cách miệng bể 0,5m. Tính chiều sâu của bể bơi.
- Bài tập 8: Một trang trại chăn nuôi cần xây một bể chứa nước có đáy hình chữ nhật 5m × 3,5m. Chi phí làm đáy bể là 8.750.000 đồng và chi phí làm tường bể là 43.200.000 đồng. Biết đơn giá xây dựng đồng nhất là 500.000 đồng/m². Tính chiều cao của bể.
- Bài tập 9: Một khu công nghiệp cần xây một bể xử lý nước thải hình hộp chữ nhật có đáy 10m × 8m. Theo quy định an toàn, chiều cao của bể không được vượt quá 3m và thể tích tối thiểu phải đạt 240m³. Tính chiều cao phù hợp của bể xử lý.
- Bài tập 10: Một hệ thống cấp nước cho một làng nghề gồm 3 bể chứa giống nhau, mỗi bể có đáy hình chữ nhật 6m × 4m. Tổng diện tích bề mặt (bao gồm cả đáy và mặt trên) của cả 3 bể là 696m². Tính chiều cao của mỗi bể và tổng thể tích nước mà hệ thống có thể chứa.
Bài tập áp dụng thực tế tính chiều cao hộp đựng đồ
- Bài tập 1: Một công ty sản xuất hộp đựng bánh có đáy hình chữ nhật kích thước 25cm × 20cm. Mỗi hộp cần sử dụng 1.750cm² vật liệu (bao gồm cả đáy và nắp). Tính chiều cao của hộp bánh.
- Bài tập 2: Một nhà thiết kế cần làm một hộp quà hình hộp chữ nhật có đáy 30cm × 20cm. Biết rằng diện tích các mặt bên của hộp là 600cm². Tính chiều cao của hộp quà.
- Bài tập 3: Một cửa hàng đóng gói cần thiết kế hộp carton hình hộp chữ nhật có thể tích 24.000cm³. Nếu đáy hộp có kích thước 40cm × 30cm, hãy tính chiều cao của hộp.
- Bài tập 4: Một công ty đồ gỗ đang sản xuất một hộp đựng trang sức có đáy hình vuông cạnh 15cm. Họ có một tấm gỗ quý diện tích 1.350cm² để làm tất cả các mặt của hộp (bao gồm cả đáy và nắp). Tính chiều cao tối đa có thể của chiếc hộp.
- Bài tập 5: Một nhà sản xuất cần thiết kế hộp đựng giày có đáy hình chữ nhật 32cm × 20cm. Biết rằng diện tích toàn phần của hộp là 2.528cm² và chiều cao của hộp ít nhất phải đạt 12cm. Hãy xác định chiều cao chính xác của hộp.
- Bài tập 6: Một cửa hàng quà tặng cần làm một hộp quà hình hộp chữ nhật từ một tấm bìa cứng hình chữ nhật có kích thước 70cm × 50cm. Nếu đáy hộp quà có kích thước 20cm × 15cm, hãy tính chiều cao tối đa có thể của hộp quà. (Gợi ý: Khi gấp tấm bìa thành hộp, cần tính cả phần đáy và các mặt bên)
- Bài tập 7: Một công ty đóng gói thực phẩm cần thiết kế hộp hình hộp chữ nhật có đáy 18cm × 12cm. Biết rằng chi phí vật liệu là 0,5 đồng/cm² và tổng chi phí làm một hộp là 756 đồng. Tính chiều cao của hộp.
- Bài tập 8: Một thùng đựng đồ hình hộp chữ nhật có đáy hình vuông cạnh 50cm. Thùng được làm từ nhựa tái chế với định mức tiêu thụ 0,3kg/m² bề mặt. Nếu mỗi thùng tiêu thụ 1,2kg nhựa, hãy tính chiều cao của thùng.
- Bài tập 9: Một cơ sở sản xuất cần thiết kế hộp đựng sản phẩm hình hộp chữ nhật có đáy 24cm × 16cm. Theo quy định vận chuyển, tổng ba kích thước (dài + rộng + cao) không được vượt quá 100cm và thể tích không quá 15.000cm³. Tính chiều cao tối đa có thể của hộp.
- Bài tập 10: Một công ty nội thất cần thiết kế một hộp đựng đồ đa năng hình hộp chữ nhật có đáy 60cm × 45cm. Biết rằng thể tích của hộp là 108.000cm³ và tỉ lệ giữa chiều cao và chiều rộng của hộp là 0,8. Kiểm tra xem các số liệu trên có phù hợp không?
Bài tập áp dụng thực tế tính chiều cao phòng học
- Bài tập 1: Một phòng học có hình dạng hình hộp chữ nhật với chiều dài 8m và chiều rộng 6m. Theo quy định về thông gió và không gian, mỗi học sinh cần có ít nhất 4m³ không khí. Nếu lớp học có 36 học sinh, hãy tính chiều cao tối thiểu của phòng học.
- Bài tập 2: Một trường học cần xây dựng một phòng học mới có diện tích sàn 56m² (dài 8m, rộng 7m). Theo quy chuẩn xây dựng, tỉ lệ giữa thể tích và diện tích sàn của phòng phải tối thiểu là 3,5m. Tính chiều cao tối thiểu của phòng học.
- Bài tập 3: Một phòng học có dạng hình hộp chữ nhật với chiều dài 10m và chiều rộng 7m. Chi phí xây dựng các bức tường (không tính trần và sàn) là 25.200.000 đồng với đơn giá 300.000 đồng/m². Tính chiều cao của phòng học.
- Bài tập 4: Một phòng học có diện tích sàn 70m² (dài 10m, rộng 7m). Theo quy định về âm học, tỉ lệ giữa thể tích phòng và diện tích bề mặt phải nằm trong khoảng từ 0,8 đến 1,2. Nếu chiều cao của phòng là 3,5m, hãy kiểm tra xem phòng học có đạt tiêu chuẩn về âm học không.
- Bài tập 5: Một trường học cần xây dựng phòng thí nghiệm có diện tích sàn 54m² (dài 9m, rộng 6m). Theo quy định an toàn, thể tích không khí cho mỗi học sinh phải tối thiểu là 5m³ và phòng thí nghiệm được thiết kế cho 25 học sinh. Tính chiều cao tối thiểu của phòng thí nghiệm.
- Bài tập 6: Một phòng học hình hộp chữ nhật có diện tích sàn 60m² (dài 10m, rộng 6m) và chiều cao 3,2m. Chi phí sơn toàn bộ tường và trần (không tính sàn) là 10.080.000 đồng. Biết đơn giá sơn là 40.000 đồng/m². Kiểm tra tính chính xác của chiều cao phòng.
- Bài tập 7: Một phòng hội trường trường học hình hộp chữ nhật có chiều dài 15m và chiều rộng 12m. Theo tiêu chuẩn thiết kế về âm thanh, thể tích tối thiểu cho mỗi chỗ ngồi là 6m³. Nếu hội trường có 120 chỗ ngồi, hãy tính chiều cao tối thiểu của hội trường.
- Bài tập 8: Một phòng học đa năng có dạng hình hộp chữ nhật với chiều dài 12m và chiều rộng 9m. Chi phí lắp đặt hệ thống điều hòa là 72 triệu đồng, với đơn giá 200.000 đồng/m³ không khí. Tính chiều cao của phòng học đa năng.
- Bài tập 9: Một phòng học tin học có dạng hình hộp chữ nhật với chiều dài 8m và chiều rộng 6m. Theo quy định chống cháy, chiều cao tối thiểu phải đạt 3m và hệ số an toàn (tỉ lệ giữa thể tích phòng và tổng diện tích bề mặt) phải lớn hơn 0,75. Tính chiều cao tối thiểu thỏa mãn cả hai điều kiện trên.
Các lưu ý khi tính chiều cao hình hộp chữ nhật
Khi tính toán chiều cao của hình hộp chữ nhật, việc thực hiện cẩn thận và chính xác là yếu tố then chốt để có được kết quả đúng. Dù các công thức tính chiều cao không quá phức tạp, nhưng trong quá trình áp dụng, chúng ta vẫn thường gặp phải những sai sót dẫn đến kết quả không chính xác. Phần này sẽ trình bày những lưu ý quan trọng giúp bạn tránh được các lỗi thường gặp, đảm bảo tính chính xác trong quá trình tính toán, và một số mẹo hữu ích để giải nhanh các bài toán liên quan đến chiều cao hình hộp chữ nhật.
Kiểm tra đơn vị đo
Một trong những yếu tố quan trọng nhất khi tính chiều cao hình hộp chữ nhật là đảm bảo tính nhất quán của đơn vị đo. Việc sử dụng sai hoặc không thống nhất đơn vị đo là nguyên nhân phổ biến dẫn đến kết quả sai lệch.
Đảm bảo tính đồng nhất của đơn vị đo: Tất cả các kích thước (chiều dài, chiều rộng, chiều cao) phải được biểu diễn bằng cùng một đơn vị đo. Ví dụ: nếu chiều dài và chiều rộng được tính bằng cm, thì chiều cao cũng phải tính bằng cm.
Chú ý đến đơn vị đo của thể tích: Nếu chiều dài, chiều rộng được đo bằng cm thì thể tích sẽ tính bằng cm³. Tương tự, nếu đo bằng m thì thể tích sẽ tính bằng m³.
Quy đổi đơn vị đo khi cần thiết: Trong nhiều bài toán thực tế, các kích thước có thể được biểu diễn bằng các đơn vị đo khác nhau. Ví dụ: chiều dài tính bằng m, chiều rộng tính bằng dm. Trong trường hợp này, cần quy đổi tất cả về cùng một đơn vị đo trước khi áp dụng công thức.
Bảng quy đổi đơn vị đo thông dụng:
- 1 m = 100 cm = 1.000 mm
- 1 dm = 10 cm = 100 mm
- 1 m³ = 1.000 dm³ = 1.000.000 cm³
- 1 lít = 1 dm³ = 1.000 cm³
Lưu ý: Với đơn vị đo diện tích: Khi tính từ diện tích xung quanh hoặc diện tích toàn phần, cần đảm bảo đơn vị đo diện tích tương thích với đơn vị đo chiều dài. Ví dụ: nếu chiều dài và chiều rộng tính bằng m, thì diện tích phải tính bằng m².
Các lỗi thường gặp
Khi giải các bài toán liên quan đến chiều cao hình hộp chữ nhật, có một số lỗi thường gặp mà người học cần tránh:
- Nhầm lẫn giữa các công thức: Áp dụng sai công thức cho từng trường hợp cụ thể. Ví dụ: sử dụng công thức tính từ diện tích xung quanh khi bài toán yêu cầu tính từ diện tích toàn phần.
- Bỏ qua yếu tố đơn vị đo: Như đã đề cập ở phần trên, việc không thống nhất đơn vị đo là nguyên nhân phổ biến dẫn đến kết quả sai.
- Nhầm lẫn giữa diện tích xung quanh và diện tích toàn phần: Diện tích xung quanh chỉ bao gồm 4 mặt bên, trong khi diện tích toàn phần bao gồm cả 6 mặt của hình hộp chữ nhật.
- Sai sót trong quá trình tính toán đại số: Khi giải phương trình để tìm chiều cao, các lỗi về phép tính, dấu số, hoặc việc biến đổi phương trình không chính xác có thể dẫn đến kết quả sai.
- Không kiểm tra tính hợp lý của kết quả: Sau khi tính toán, cần kiểm tra xem kết quả có hợp lý không. Ví dụ: chiều cao của một bể nước không thể là một số âm hoặc quá nhỏ so với thực tế.
- Bỏ qua các ràng buộc trong bài toán: Nhiều bài toán thực tế có các ràng buộc về kích thước tối đa, tối thiểu, hoặc các điều kiện khác. Việc bỏ qua các ràng buộc này có thể dẫn đến kết quả không khả thi trong thực tế.
- Nhầm lẫn trong việc xác định chiều cao: Trong một số trường hợp, có thể nhầm lẫn về việc chiều nào là chiều cao của hình hộp chữ nhật, đặc biệt khi hình hộp được đặt ở các vị trí khác nhau.
Mẹo giải nhanh
Dưới đây là một số mẹo giúp giải nhanh các bài toán liên quan đến chiều cao hình hộp chữ nhật:
- Phân tích bài toán trước khi giải: Xác định rõ dữ kiện và yêu cầu của bài toán, từ đó chọn công thức phù hợp nhất để giải.
- Sử dụng công thức trực tiếp cho các trường hợp phổ biến:
- Khi biết thể tích: h = V / (a × b)
- Khi biết diện tích xung quanh: h = Sxq / [2(a + b)]
- Khi biết diện tích toàn phần: h = (S – 2ab) / [2(a + b)]
- Áp dụng phương pháp thay thế nhanh: Đối với các bài toán phức tạp, có thể áp dụng phương pháp thay thế để đơn giản hóa quá trình tính toán. Ví dụ: nếu biết a + b = P và ab = Q, thì 2(a + b) = 2P và 2ab = 2Q.
- Kiểm tra nhanh tính hợp lý: Sử dụng ước lượng để kiểm tra nhanh tính hợp lý của kết quả. Ví dụ: nếu tính được chiều cao của một phòng học là 0,5m, rõ ràng đây là kết quả không hợp lý và cần kiểm tra lại các bước tính.
- Sử dụng tỉ lệ kích thước: Trong nhiều bài toán, các kích thước của hình hộp chữ nhật có mối quan hệ tỉ lệ với nhau. Việc nhận biết mối quan hệ này có thể giúp giải nhanh bài toán.
- Tận dụng các mối quan hệ đặc biệt: Ví dụ, nếu hình hộp chữ nhật có đáy là hình vuông (a = b), các công thức sẽ trở nên đơn giản hơn:
- h = V / a²
- h = Sxq / (4a)
- h = (S – 2a²) / (4a)
- Đổi đơn vị đo từ sớm: Thay vì đợi đến bước cuối mới đổi đơn vị, hãy đổi tất cả các đơn vị về dạng chuẩn ngay từ đầu để tránh sai sót.
- Sử dụng máy tính hỗ trợ: Đối với các phép tính phức tạp, việc sử dụng máy tính có thể giúp tiết kiệm thời gian và giảm thiểu sai sót trong quá trình tính toán.
Áp dụng những mẹo trên sẽ giúp bạn giải nhanh và chính xác các bài toán về chiều cao hình hộp chữ nhật, từ đó nâng cao hiệu quả học tập và áp dụng vào các tình huống thực tế.
Kết luận
Tính chiều cao hình hộp chữ nhật là một kỹ năng quan trọng. Kỹ năng này không chỉ cần thiết trong học tập mà còn hữu ích trong nhiều tình huống thực tế. Trong bài viết này, bạn đã biết chiều cao là gì và cách xác định chiều cao của hình hộp chữ nhật. Bạn cũng đã học các công thức tính chiều cao trong nhiều trường hợp khác nhau, như khi biết thể tích, diện tích xung quanh hoặc diện tích toàn phần. Bài viết còn có nhiều bài tập từ dễ đến khó, nhất là các bài toán thực tế như thiết kế bể nước, hộp đựng đồ hay phòng học. Ngoài ra, bạn đã được nhắc nhở về đơn vị đo, các lỗi thường gặp và mẹo giải nhanh. Hy vọng những kiến thức này từ Hoc2K sẽ giúp bạn tự tin hơn khi làm bài tập và áp dụng vào cuộc sống.
