Bạn đang tìm kiếm công thức tính thể tích hình hộp chữ nhật một cách chính xác, dễ hiểu và đầy đủ nhất? Bài viết này từ Hoc2K sẽ giúp bạn cách xác định đúng các cạnh, các đơn vị đo thể tích chuẩn quốc tế và những lưu ý quan trọng khi áp dụng công thức vào thực tế. Dù bạn là học sinh đang cần ôn tập kiến thức, một kỹ sư cần tính toán nhanh chi phí vật liệu, hay chỉ đơn giản là muốn kiểm soát không gian lưu trữ hiệu quả, đây chính là hướng dẫn toàn diện nhất dành cho bạn.
Thể tích hình hộp chữ nhật là gì?
Thể tích hình hộp chữ nhật là đại lượng đo phần không gian mà khối hộp đó chiếm trong thực tế, thường được biểu diễn bằng các đơn vị như cm3 , dm3 hoặc m3 ,Trong hình học và đời sống, khái niệm này xuất hiện rất nhiều khi cần đánh giá “chứa được bao nhiêu” nước, không khí hay vật liệu trong một vật có dạng hộp.
Việc nắm vững công thức tính thể tích hình hộp chữ nhật giúp học sinh giải nhanh, đúng các bài tập Toán từ Tiểu học đến THCS, đặc biệt là các dạng bài thực tế trong sách giáo khoa. Ngoài ra, người lớn có thể ứng dụng để tính dung tích bể nước, thùng hàng, thể tích phòng hoặc kho chứa nhằm ước lượng lượng nước, hàng hóa hay vật liệu cần dùng cho sinh hoạt và công việc.
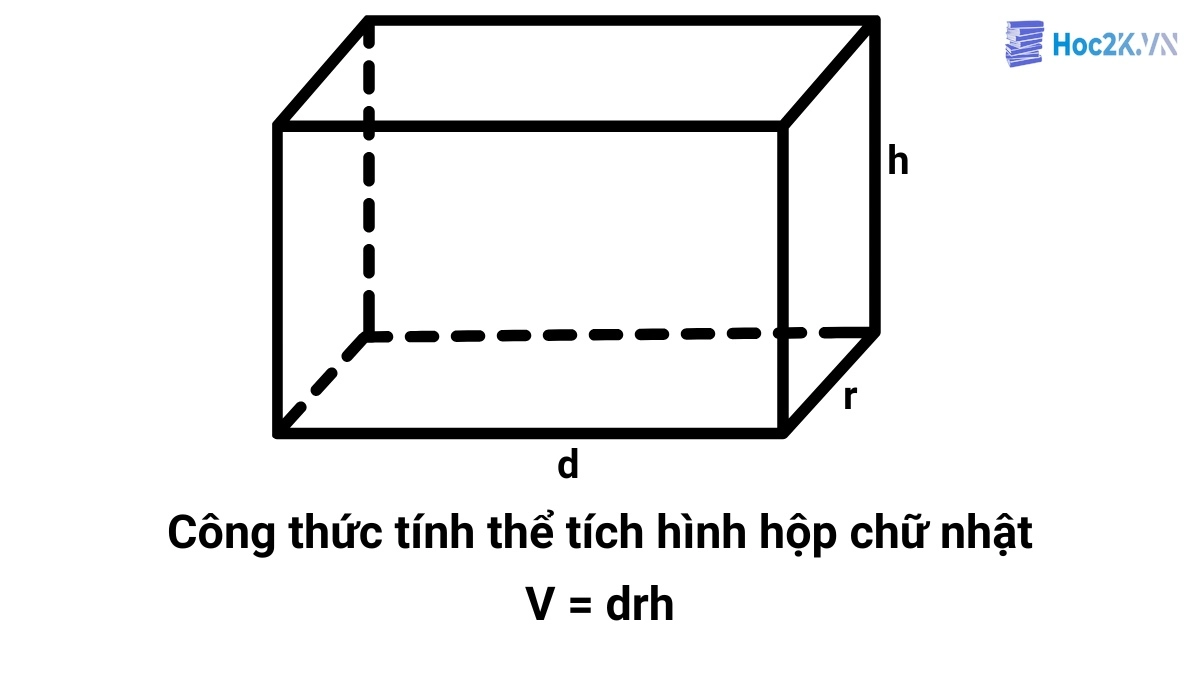
Công thức tổng quát tính thể tích hình hộp chữ nhật
Công thức tính thể tích hình hộp chữ nhật bằng chiều dài nhân với chiều rộng và nhân với chiều cao của hình hộp chữ nhật (cùng đơn vị đo). Công thức này áp dụng cho cả hình hộp chữ nhật có nắp và không có nắp, vì tính thể tích chỉ liên quan đến không gian bên trong hình, không phụ thuộc vào việc có nắp hay không có nắp.
Cách tính thể tích hình hộp chữ nhật: V = d × r × h
Trong đó
- V: Thể tích hình hộp chữ nhật
- d: Chiều dài mặt đáy
- r: Chiều rộng mặt đáy
- h: Chiều cao
Đơn vị tính thể tích hình hộp chữ nhật
Đơn vị thể tích hình hộp chữ nhật sẽ phụ thuộc vào đơn vị của các chiều. Nếu chiều dài, chiều rộng và chiều cao được đo bằng mét (m), thì thể tích sẽ có đơn vị là mét khối (m³). Nếu các chiều được đo bằng centimet (cm), thì thể tích sẽ có đơn vị là centimet khối (cm³).
Cách tính thể tích hình hộp chữ nhật qua từng bước
Bước 1: Xác định các kích thước d, r, h
- Từ đề bài hoặc từ thực tế (khi đo), xác định ba kích thước: chiều dài d, chiều rộng r, chiều cao h của hình hộp chữ nhật.
- Ghi lại kèm đơn vị: ví dụ d = 5 cm, r = 3 cm, h = 4 cm để dễ thao tác ở bước sau.
Bước 2: Quy đổi về cùng một đơn vị
- Nếu các kích thước đang ở các đơn vị khác nhau (vd: d tính bằng cm, r bằng dm, h bằng m), cần đổi về cùng một đơn vị trước khi nhân.
- Thường trong chương trình phổ thông, giáo viên khuyến khích quy đổi hết về cm hoặc m để kết quả dễ so sánh và vận dụng.
Bước 3: Thay số vào công thức và ghi đơn vị
- Áp dụng công thức: V = d × r × h và sau đó thay số, thực hiện phép nhân.
- Cuối cùng kết luận bằng câu đầy đủ, kèm đơn vị thể tích như cm3, dm3, hoặc m3.
Ví dụ minh họa
Dưới dây là bài tập ví dụ giúp học các em học sinh dễ dàng làm theo và áp dụng công thức.
Đề bài (cơ bản): Cho hình hộp chữ nhật có chiều dài 9cm, chiều rộng 6cm và chiều cao là 5cm. Thể tích của hình hộp chữ nhật này là bao nhiêu?
Bài giải: Áp dụng công thức tính thể tích ta có: V = 9 x 6 x 5 = 270 (cm3)
Đáp số: 270 (cm3)
Các dạng bài tập từ cơ bản đến nâng cao tính thể tích hình hộp chữ nhật có lời giải
Dưới đây là các dạng bài tập toán có sử dụng công thức thể tích hình hộp chữ nhật mà các bạn học sinh thường gặp:
Tính thể tích hình hộp chữ nhật khi biết chiều dài, chiều rộng và chiều cao
Ví dụ: Tính thể tích của một hộp chữ nhật có chiều dài 6cm, chiều rộng 5cm và chiều cao 7cm.
Bài giải:
Áp dụng công thức tính thể tích ta có: V = 6 x 5 x 7 = 210 (cm3)
Đáp số: 210 (cm3)
Tính chiều dài khi đã biết được chiều rộng, chiều cao và thể tích hình hộp chữ nhật
Ví dụ: Tính chiều dài hình hộp chữ nhật có thể tích là 210 (cm3), chiều rộng 5 cm và chiều cao 7cm.
Bài giải:
Áp dụng công thức tính thể tích ta có: 210 = d x 5 x 7 = 6 cm
Đáp số: 6 cm
Tính chiều rộng khi đã biết được chiều dài, chiều cao và thể tích hình hộp chữ nhật
Ví dụ: Tính chiều rộng hình hộp chữ nhật có thể tích là 210 (cm3), chiều dài 6 cm và chiều cao 7cm.
Bài giải:
Áp dụng công thức tính thể tích ta có: 210 = 6 x r x 7 = 5 cm
Đáp số: 5 cm
Tính chiều cao khi đã biết được chiều dài, chiều rộng và thể tích hình hộp chữ nhật
Ví dụ: Tính chiều cao hình hộp chữ nhật có thể tích là 210 (cm3), chiều dài 6 cm và chiều rộng 5cm.
Bài giải:
Áp dụng công thức tính thể tích ta có: 210 = 6 x 5 x h = 7 cm
Đáp số: 7 cm
Tính thể tích hình hộp chữ nhật được cắt bỏ một phần
Ví dụ: Tính thể tích của một hộp chữ nhật có chiều dài 15cm, chiều rộng 9cm và chiều cao 7cm nếu một phần của hộp bị cắt bỏ là hình lập phương có cạnh là 4cm.
Bài giải:
V = d x r x h
V = (15 x 9 x 7) – (4 x 4 x 4)
=> V = 945 – 64 = 881 (cm3)
Đáp số: 881 (cm3)
Tính thể tích của một hộp chữ nhật có một lỗ hình tròn được đục ra khỏi một mặt phẳng của nó
Ví dụ: Tính thể tích của một hộp chữ nhật có chiều dài 9cm, chiều rộng 8cm và chiều cao 6cm nếu một lỗ hình tròn bán kính 2cm được đục ra khỏi một mặt phẳng của nó.
Bài giải:
V = d x r x h => V = (9 x 8 x 6) – (pi x 22 x 6)
V = 432 – 75.36 = 356.6 (cm3)
Đáp số: 356.6 (cm3)
Tính thể tích hình hộp chữ nhật không đều, có các mặt phẳng lệch nhau
Ví dụ: Tính thể tích của một hộp chữ nhật không đều, có chiều dài 14cm, chiều rộng 9cm và chiều cao 7cm. Mặt phẳng dưới cùng của hộp là một hình tam giác đều với cạnh 6cm.
Bài giải:
V = d x r x h => V = (14 x 9 x 7) + (1/2 x 6 x 4)
V = 882 + 12 = 894 (cm3)
Đáp số: 894 (cm3)
Ứng dụng thể tích hình hộp chữ nhật trong thực tế
Công thức tính thể tích hình hộp chữ nhật không chỉ là lý thuyết mà còn được áp dụng rộng rãi trong học tập và đời sống hàng ngày, giúp giải quyết các vấn đề thực tiễn một cách chính xác và hiệu quả.
Trong học tập
Hình hộp chữ nhật là một trong những khối cơ bản được giảng dạy từ Toán lớp 5 đến lớp 7-8 trong chương trình phổ thông, giúp học sinh làm quen với khái niệm thể tích và cách áp dụng công thức vào bài tập. Kiến thức này tạo nền tảng vững chắc để học các khối phức tạp hơn như lăng trụ đứng, hình chóp cụt hay hình hộp chữ nhật bị khoét, nơi thể tích thường được tính bằng tổng hoặc hiệu các thể tích hình hộp chữ nhật.
Trong đời sống
Trong sinh hoạt đời sống thể tích hình hộp chữ nhật giúp tính dung tích bể nước gia đình, bể cá cảnh hoặc hồ bơi hình hộp để biết lượng nước cần bơm đầy hoặc thay định kỳ. Ngoài ra, nó còn dùng để ước lượng thể tích phòng ở, kho hàng, container vận chuyển hay thùng carton đóng gói, từ đó tính chi phí vận chuyển, sắp xếp hàng hóa hoặc lượng không khí cần điều hòa.
Xem thêm các nội dung liên quan:
- Cách tính chiều rộng hình hộp chữ nhật: Công thức, ví dụ và bài tập
- Cách tính chiều cao hình hộp chữ nhật: Công thức, ví dụ và bài tập
- Cách tính đường chéo hình hộp chữ nhật: Công thức, ví dụ và bài tập
- Cách tính chu vi mặt đáy hình hộp chữ nhật: Công thức, ví dụ và bài tập
- Cách tính diện tích xung quanh hình hộp chữ nhật: Công thức, ví dụ và bài tập
- Cách tính diện tích toàn phần hình hộp chữ nhật: Công thức ví, dụ và bài tập
Kết luận
Trên đây là công thức và các dạng bài tập về thể tích hình hộp chữ nhật, giúp học sinh nắm chắc kiến thức cơ bản và áp dụng linh hoạt vào giải toán cách tính thể tích hình hộp chữ nhật. Hy vọng qua bài viết này Hoc2K đã có thể giúp các bạn có thể tự tin hơn khi gặp các bài toán liên quan và tiếp tục rèn luyện để nâng cao kỹ năng. Chúc các bạn học tốt!