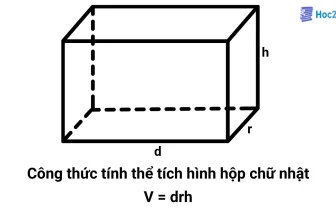
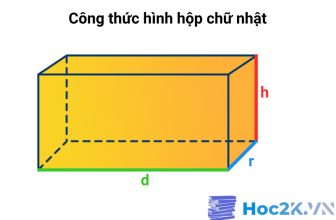
Diện tích hình hộp chữ nhật là một trong những khái niệm cơ bản và quan trọng trong hình học, thường gặp trong chương trình toán học phổ thông. Việc nắm vững công thức tính diện tích hình hộp chữ nhật không chỉ giúp học sinh giải quyết các bài toán một cách hiệu quả mà còn tạo nền tảng vững chắc cho những kiến thức nâng cao hơn khi gặp các bài toán về hình hộp chữ nhật. Bài viết này từ Hoc2K sẽ giới thiệu công thức tính diện tích hình hộp chữ nhật, đồng thời cung cấp các dạng bài tập từ cơ bản đến nâng cao để các bạn học sinh có thể thực hành và củng cố kiến thức một cách toàn diện.
Diện tích hình hộp chữ nhật là gì?
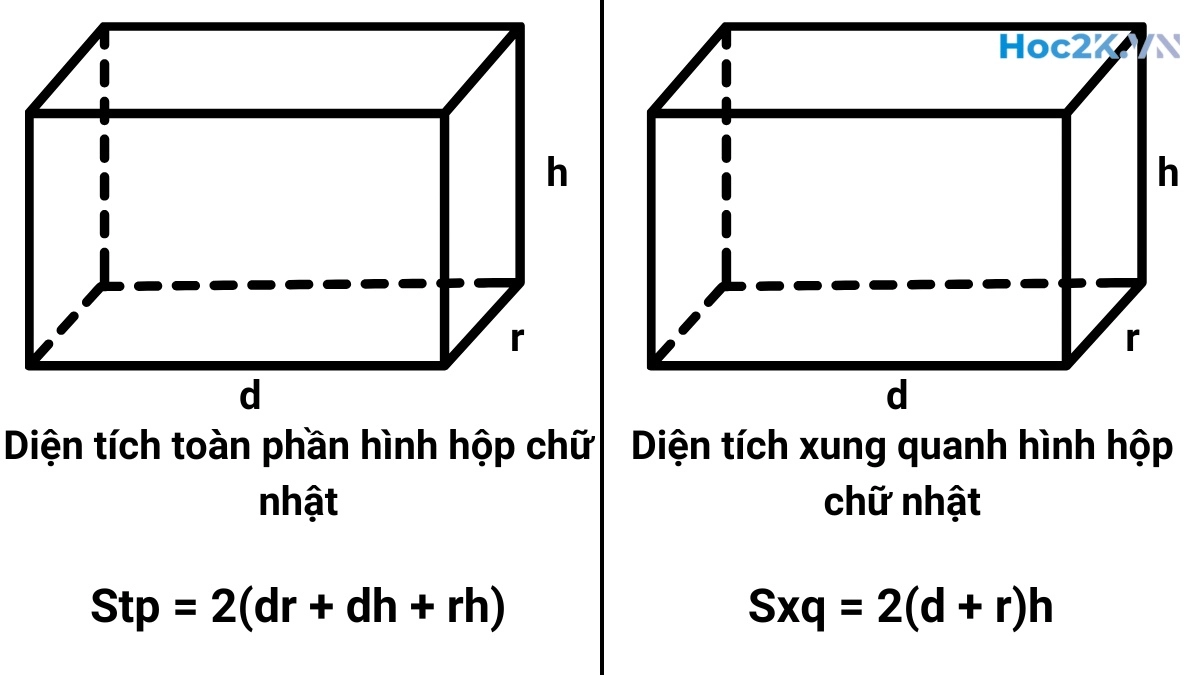
Diện tích hình hộp chữ nhật có hai loại: Diện tích xung quanh và diện tích toàn phần. Diện tích xung quanh là phần diện tích của 4 mặt bên, tức là chỉ tính phần “thân” của hình hộp, không tính hai mặt đáy. Còn diện tích toàn phần là diện tích của toàn bộ hình hộp, bao gồm cả 4 mặt bên và 2 mặt đáy, tức là tính cả thân và đáy.
Đơn vị đo diện tích hình hộp chữ nhật
Đơn vị đo diện tích phổ biến trong hình hộp chữ nhật là cm², m² hoặc đơn vị diện tích phù hợp với đề bài. Khi thực hiện phép tính, bắt buộc phải đổi tất cả các đại lượng về cùng một hệ đơn vị trước khi áp dụng công thức. Sau khi tính xong, kiểm tra lại đơn vị kết quả đại diện cho diện tích.
Các công thức tính diện tích hình hộp chữ nhật
Công thức tính diện tích xung quanh hình hộp chữ nhật
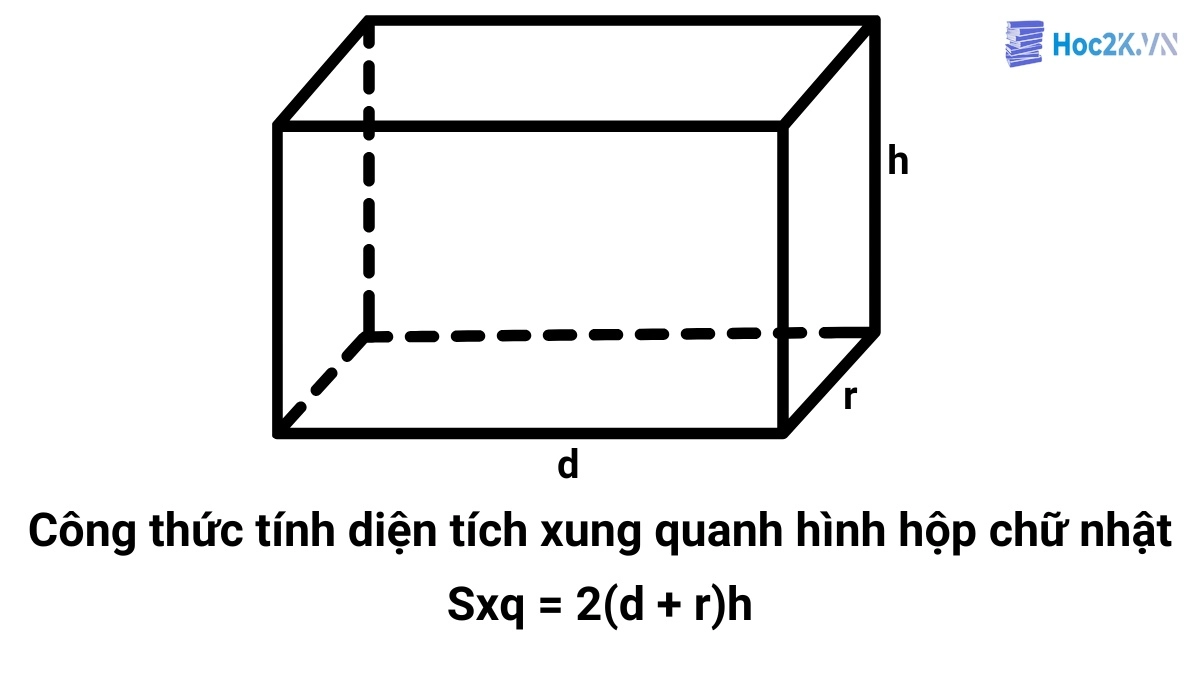
Để tính diện tích xung quanh hình hộp chữ nhật ta lấy chu vi đáy nhân với chiều cao (Chu vi đáy bằng hai nhân với tổng của chiều dài và chiều rộng). Phép tính này thường xuất hiện trong chương trình Toán tiểu học, đặc biệt ở lớp 5, đồng thời được sử dụng rộng rãi trong đời sống thực tế và sản xuất.
Việc tính chính xác chu vi mặt đáy là bước căn bản để xác định diện tích xung quanh ở bước tiếp theo. Chu vi này cũng có thể xem như tổng chiều dài đường viền bao quanh hình chữ nhật ở mặt đáy.
![\[S_{xq}=\;2\;\times\;\left(d\;+\;r\right)\;\times\;h\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-72143e14642b0f40ffb4a43be645f185_l3.png "Rendered by QuickLaTeX.com")
d: Chiều dài hình hộp chữ nhật
r: Chiều rộng hình hộp chữ nhật
h: Chiều cao hình hộp chữ nhật
Ví dụ cách tính diện tích xung quanh hình hộp chữ
Đề bài: Một hình hộp chữ nhật có chiều dài d = 6cm, chiều rộng r = 4cm, chiều cao h = 10cm. Tính diện tích xung quanh hình hộp này.
Lời giải:
Bước 1: Tính chu vi mặt đáy
![\[P_{đáy}=\;2\;\times\;(d\;+\;r)\;=\;2\;\times\;(6\;+\;4)\;=\;2\;\times\;10\;=\;20\;cm\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-39dd66d26f0e2baf3e8c8b5005924517_l3.png "Rendered by QuickLaTeX.com")
Bước 2: Nhân chu vi đáy với chiều cao
![\[S_{xq}\;=\;P_{đáy}\;\times\;h\;=\;20\;\times\;10\;=\;200\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-2d2c681638f809c65ef2daadc7b5aae9_l3.png "Rendered by QuickLaTeX.com")
Đáp số: Diện tích xung quanh hình hộp chữ nhật là 200 cm².
Các bài tập tự luyện tính diện tích xung quanh hình hộp chữ nhật tại nhà
Một hình hộp chữ nhật có chiều dài 8 cm, chiều rộng 5 cm, chiều cao 6 cm. Tính diện tích xung quanh.
Đáp án:
![\[S_{xq}=2\times6\times(8+5)=156\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-af258cafd79b84fc9e1c3be8be493c52_l3.png "Rendered by QuickLaTeX.com")
Hình hộp chữ nhật với d = 10 cm, r = 4 cm, h = 12 cm. Tìm diện tích xung quanh.
Đáp án:
![\[2\times12\times(10+4)=336\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-a0ec3402063526ef7d6696fe7e6fb381_l3.png "Rendered by QuickLaTeX.com")
Tính diện tích xung quanh của hình hộp chữ nhật có d = 7 dm, r =3 dm , h = 4 dm.
Đáp án:
![\[2\times4\times(7+3)=80\;dm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-29cbe1c98761c850ca758a131a42102a_l3.png "Rendered by QuickLaTeX.com")
Chiều dài d = 0,8 m, chiều rộng r = 0,6 m, chiều cao h = 1,2 m. Sxq bằng bao nhiêu?
Đáp án:
![\[2\times1,2\times(0,8+0,6)=2,88\;m^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-1c35d4d2429d15a848a2fb8e7da5812d_l3.png "Rendered by QuickLaTeX.com")
d = 25cm, r = 17 cm, h = 9 cm. Hỏi diện tích xung quanh.
Đáp án:
![\[2\times9\times(25+17)=2\times9\times42=756\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-68938890e0629e5d8481f088e9f09717_l3.png "Rendered by QuickLaTeX.com")
Một thùng giấy: d = 15 cm, r = 20 cm, h = 30 cm. Tìm Sxq.
Đáp án:
![\[2\times30\times(15+20)=2\times30\times35=2,100\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-ab482bbbcfcfe75d9cc566bde6a8afab_l3.png "Rendered by QuickLaTeX.com")
Hình hộp chữ nhật: d = 6 cm, r = 5 cm, h = 9 cm. Diện tích xung quanh là?
Đáp án:
![\[2\times9\times(6+5)=2\times9\times11=198\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-dd6a5ae89867e4d9e5a5865110d4bd50_l3.png "Rendered by QuickLaTeX.com")
Nếu d = 12 dm, r = 7 dm, h = 8 dm. Sxq bằng?
Đáp án:
![\[2\times8\times(12+7)=2\times8\times19=304\;dm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-69d21973c3a4e17b7d0a80ddaa969fe4_l3.png "Rendered by QuickLaTeX.com")
Hình hộp có d = 9 cm, r = 4 cm, h = 10 cm. Diện tích xung quanh là:
Đáp án:
![\[2\times10\times(9+4)=2\times10\times13=260\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-1d262cdc052af6a7bbe49595e82811a8_l3.png "Rendered by QuickLaTeX.com")
Một hộp quà: d = 13 cm, r = 9 cm, h = 6 cm. Tìm diện tích xung quanh.
Đáp án:
![\[2\times6\times(13+9)=2\times6\times22=264\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-debf08433023d774857f2d84b806e327_l3.png "Rendered by QuickLaTeX.com")
Hình hộp chữ nhật có diện tích xung quanh Sxq = 220 cm2, chiều dài d = 10 cm, chiều rộng r = 6 cm. Tìm chiều cao h.
Đáp án:
![\[h=\frac{220}{2\times(10+6)}=\frac{220}{32}=6.875\;cm\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-d74dcc6743da765baf9d125cf1c37000_l3.png "Rendered by QuickLaTeX.com")
Một bể cá có chiều cao là 12 cm, diện tích xung quanh là 480 cm2, chiều dài hơn chiều rộng 4 cm, chiều dài là d, chiều rộng là r. Biết d + r = x. Tìm d, r.
Hướng dẫn: Đặt d = r + 4, 2h(d + r) = 480; 2 x 12 x (r + 4 +r) = 480
Hình hộp chữ nhật có diện tích xung quanh gấp đôi diện tích đáy. Biết d = 8 cm, r = 7 cm, tìm h.
Đáp án:
![\[S_{xq}=2S_{đáy}\rightarrow2h(d+r)=2dr\rightarrow h(d+r)=dr\rightarrow h=\frac{dr}{d+\;r}=\frac{8\times7}{15}=\frac{56}{15}\approx3.73\;cm\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-1f8bb57316fc69767b0dbbdf0ed4ca6f_l3.png "Rendered by QuickLaTeX.com")
Một khối hộp có d, r, h đều là số nguyên, d + r = 17 cm, h = 6 cm, diện tích xung quanh là Sxq = 204 cm2. Tìm d, r.
Đáp án:
![\[S_{xq}=2h(d+r)=2\times6\times17=204\;cm^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-18a16e4c8170c4960b5a631b597e0095_l3.png "Rendered by QuickLaTeX.com")
Hộp carton có chiều dài gấp 3 lần chiều rộng, chiều cao bằng chiều rộng, diện tích xung quanh là 480 cm2. Tìm kích thước các cạnh.
Gọi r là x, d = 3x, h = x
Đáp án:
![\[S_{xq}=2h(d+r)\;=\;2x(3x+x)\;=2x(3x+x)\;=2x\times4x\;=8x^2=480\;\Rightarrow x\approx\sqrt{60}\approx7.75\mathrm{cm}\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-c5db22f101b719f97a3b859518740337_l3.png "Rendered by QuickLaTeX.com")
![\[\begin{array}{c}a\approx3x=3\times7.75\mathrm{cm}\b\approx x=7.75\mathrm{cm}\h\approx x=7.75\mathrm{cm}\end{array}\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-e3e9abb2cc3004bd7b036d4190eab496_l3.png "Rendered by QuickLaTeX.com")
Tính diện tích decal cần dán bốn mặt bên ngoài của một bể cá có kích thước d = 80 cm, r = 40 cm, h = 50cm.
Đáp án:
![\[2\times50\times(80+40)=2\times50\times120=12,000\;cm^2=1.2\;m^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-9f616978ca0adc037926c0288482db28_l3.png "Rendered by QuickLaTeX.com")
Một kho chứa có kích thước d =12 m, r = 5 m, h = 3 m. Tính diện tích sơn cần sơn bốn vách tường.
Đáp án:
![\[2\times3\times(12+5)=2\times3\times17=102\;m^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-79c7e4963a1f47203eca35534a66834e_l3.png "Rendered by QuickLaTeX.com")
Một thùng tôn đặc có chiều dài 3 m, chiều rộng 1.2 m, cao 0.7 m. Tính diện tích cần dùng để làm 4 mặt bên ngoài.
Đáp án:
![\[2\times0.7\times(3+1.2)=2\times0.7\times4.2=5.88\;m^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-367fa43ee94b880ae01f5c453b0bdda0_l3.png "Rendered by QuickLaTeX.com")
Một phòng học hình hộp chữ nhật không có cửa sổ, dài 8 m, rộng 6 m, cao 3.4 m. Muốn dán giấy quanh bốn bức tường, cần bao nhiêu m² giấy?
Đáp án:
![\[2\times3.4\times(8+6)=2\times3.4\times14=95.2\;m^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-81eb3f850d28248c4cade599a620ccd7_l3.png "Rendered by QuickLaTeX.com")
Công ty muốn sản xuất bìa nhựa bọc ngoài thùng carton (d = 0.5 m,b = 0.35 m, h = 0.6 m). Tính diện tích nhựa cần dùng.
Đáp án:
![\[2\times0.6\times(0.5+0.35)=2\times0.6\times0.85=1.02\;m^2\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-eacb292ccd11dbc7fdad5c31cacd2b46_l3.png "Rendered by QuickLaTeX.com")
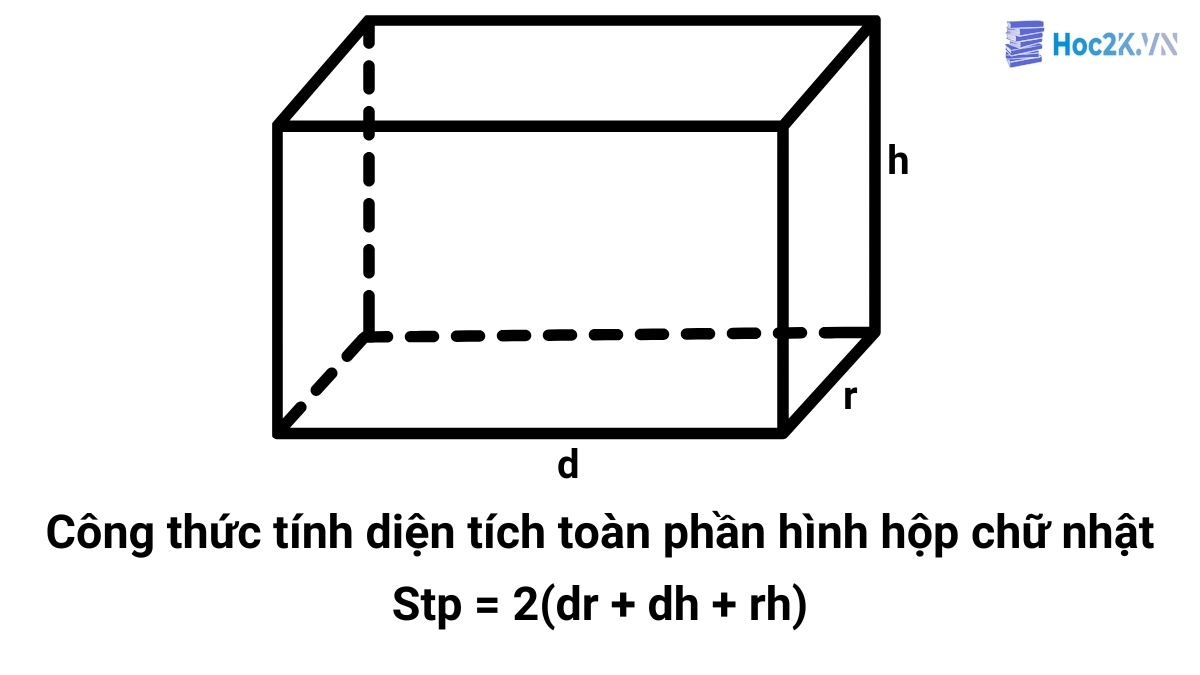
Công thức tính diện tích toàn phần hình hộp chữ nhật
Diện tích toàn phần của hình hộp chữ nhật bằng tổng diện tích của tất cả các mặt (bao gồm cả các mặt bên và hai đáy).
Công thức 1
![\[S_{tp}=\;2\;\times\;\left(dr\;+\;dh\;+\;rh\right)\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-6629f50db5e6ea9d751fc1edfd75382d_l3.png "Rendered by QuickLaTeX.com")
Công thức 2
![\[S_{tp}=\;2h\left(d\;+\;r\right)\;+\;2dr\]](https://hoc2k.vn/wp-content/ql-cache/quicklatex.com-e54cd691e9a3e19c3aec45c83f9798e4_l3.png "Rendered by QuickLaTeX.com")
d: Chiều dài của đáy hộp chữ nhật
r: Chiều rộng của đáy hộp chữ nhật
h: Chiều cao hình hộp chữ nhật
Ví dụ cách tính diện tích toàn phần hình hộp chữ
Đề bài: Cho hình hộp chữ nhật có chiều dài là 10 cm, chiều rộng là 5 cm, chiều cao là 7 cm. Hãy tính diện tích toàn phần của hình hộp chữ nhật
Bài giải:
Diện tích toàn phần hình hộp chữ nhật là: Stp= 2 (10 x 5 + 10 x 7 + 5 x 7) = 310 (cm2)
Đáp số: 310 (cm2
Các bài tập tự luyện tính diện tích toàn phần hình hộp chữ nhật tại nhà
Tính diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.
Tính diện tích toàn phần của hình hộp chữ nhật có chiều dài 5dm, chiều rộng 4dm, chiều cao 3dm.
Một hình hộp chữ nhật có các kích thước: dài 18cm, rộng 13cm, cao 9cm. Tính diện tích toàn phần của hình hộp chữ nhật đó.
Tính diện tích toàn phần của hình hộp chữ nhật có chiều dài 6dm, chiều rộng 4dm, chiều cao 8dm.
Một hình hộp chữ nhật có đáy là hình vuông cạnh 7cm, chiều cao 10cm. Tính diện tích toàn phần.
Cho hình hộp chữ nhật có chiều dài 15cm, chiều rộng 8cm, chiều cao 5cm. Tính diện tích toàn phần.
Hình hộp chữ nhật có chiều dài 12cm, chiều rộng 6cm, chiều cao 10cm. Tính diện tích toàn phần.
Tính diện tích toàn phần của hình hộp chữ nhật có chiều dài 18dm, chiều rộng 1,5m, chiều cao 16dm. (lưu ý đổi đơn vị về dm)
Hình hộp chữ nhật có chiều dài gấp 3 lần chiều rộng, dài hơn chiều cao 5cm, chiều rộng 4,25cm. Tính diện tích toàn phần.
Hình hộp chữ nhật có chiều dài 23dm, chiều rộng 16dm, chiều cao 11,5dm. Tính diện tích toàn phần.
Một bể cá không nắp có chiều dài 3dm, chiều rộng 1,2dm, chiều cao 1,5dm. Tính diện tích tấm kính cần dùng để làm bể.
Một hình hộp chữ nhật có các kích thước tỉ lệ 3:4:5, thể tích là 480m³. Tìm diện tích toàn phần của hình hộp đó.
Một khu đất hình chữ nhật có chiều dài hơn chiều rộng 20m, chu vi 180m, xung quanh xây tường cao 2m. Hỏi diện tích toàn phần tường xây quanh khu đất?
Hình hộp chữ nhật có diện tích đáy 81cm², bằng 1/5 diện tích toàn phần. Tìm chiều cao?
Một cái hộp không nắp có chiều dài 40cm, rộng 30cm, cao 20cm. Tính diện tích bìa cần dùng để làm hộp.
Một căn phòng dạng hình hộp chữ nhật dài 4,5m, rộng 2m, cao 2,5m. Chủ nhà cần dán giấy lên 4 tường và trần, tổng diện tích các cửa là 5m². Tính diện tích giấy dán cần dùng.
Một xưởng bánh cần sản xuất 30,000 hộp dạng hình hộp chữ nhật, đáy là hình vuông cạnh 25cm, cao 6cm, mép dán chiếm 8% diện tích. Tính tổng diện tích bìa cần dùng.
Một thùng tôn không nắp (hình hộp chữ nhật) dài 6dm, rộng 4dm, cao 9dm. Tính diện tích tôn dùng để làm thùng.
Một viên gạch hình hộp chữ nhật dài 22cm, rộng 10cm, cao 5,5cm. Tính diện tích toàn phần cho 6 viên gạch xếp sát nhau thành 1 khối lớn (không tính mặt tiếp xúc).
Một căn phòng dài 9m, rộng 6m, cao 4m. Cần quét vôi các tường và trần, diện tích cửa là 11,25m². Tính diện tích cần quét vôi.
Kết luận
Trên đây là tổng hợp đầy đủ nhất về Công thức tính diện tích xung quanh và toàn phần hình hộp chữ nhật, giúp học sinh nắm chắc kiến thức cơ bản và áp dụng linh hoạt vào giải toán cách tính diện tích hình hộp chữ nhật. Hy vọng qua bài viết này Hoc2K đã có thể giúp các bạn có thể tự tin hơn khi gặp các bài toán liên quan và tiếp tục rèn luyện để nâng cao kỹ năng. Chúc các bạn học tốt!
