Trang chủ » Công thức Toán » Chiều rộng hình chữ nhật
Công thức Toán

Cách tính chiều rộng hình chữ nhật: Công thức, ví dụ và bài tập

Tuấn Kiệt Tuấn Kiệt
06/01/2026
15 Views 0

Chiều rộng hình chữ nhật là đại lượng thường gặp trong các bài toán hình học cơ bản. Việc nắm vững cách tính chiều rộng hình chữ nhật kết hợp với ví dụ minh họa dễ hiểu và bài tập vận dụng, sẽ giúp học sinh nhanh chóng giải đúng bài toán và tránh sai sót khi làm bài. Trong bài viết này, Hoc2K sẽ được hướng dẫn chi tiết từng phương pháp tính chiều rộng hình chữ nhật theo chu vi, diện tích và các dữ kiện liên quan, kèm theo bài tập để các em học sinh tự luyện tập hiệu quả.

Chiều rộng hình chữ nhật là gì?

Chiều rộng của hình chữ nhật là cạnh ngắn hơn (hoặc cạnh dọc) được sử dụng để tính chu vi, nửa chu vi, diện tích và chiều dài của hình chữ nhật.

Công thức tính chiều rộng hình chữ nhật
Công thức tính chiều rộng hình chữ nhật

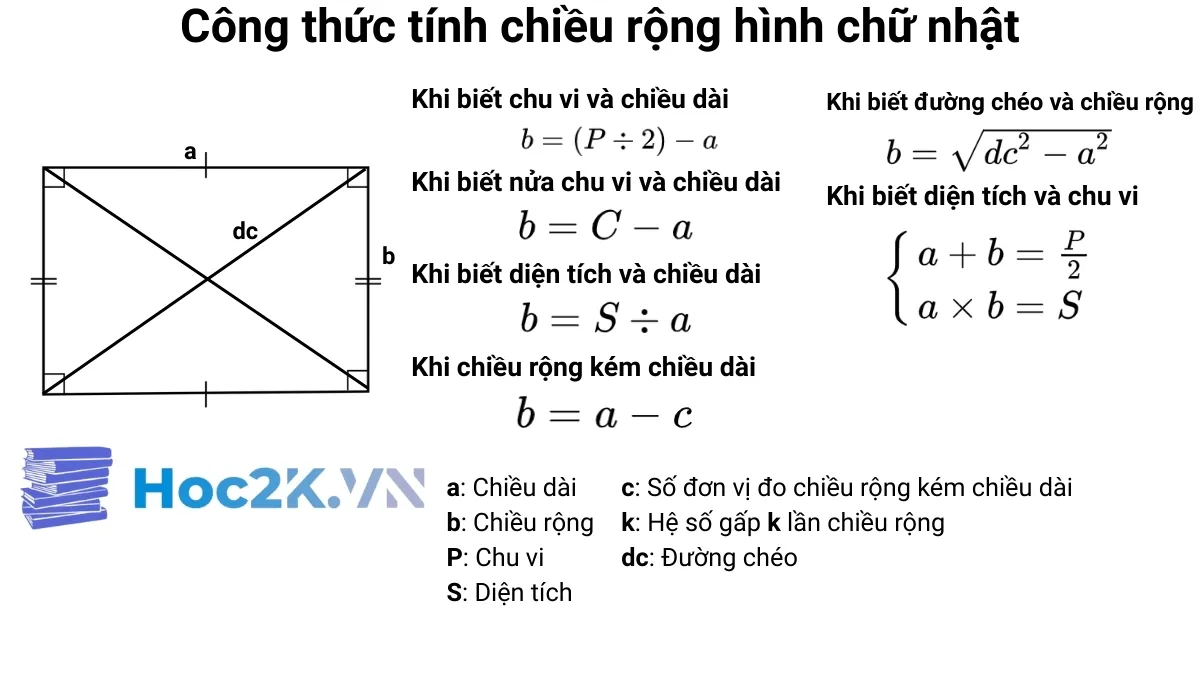
Các công thức tính chiều rộng hình chữ nhật

Dưới đây là các công thức về cách tính chiều rộng hình chữ nhật mà em học sinh thường gặp. Đề bài thường yêu cầu học sinh tính chiều rộng hình chữ nhật khi biết được một vài dữ liệu sau:

Công thức tính chiều rộng hình chữ nhật khi biết chu vi và chiều dài

Cách tính chiều rộng hình chữ nhật khi biết chu vi và chiều dài ta lấy chu vi chia 2 rồi sau đó trừ đi chiều dài.

Công thức:

b=(P÷2)−ab=(P\div 2)- a

Trong đó:

  • P: Chu vi hình chữ nhật thường có đơn vị thường là m, dm, cm,…
  • a: Chiều dài
  • b: Chiều rộng

Ví dụ cách tìm chiều rộng của hình chữ nhật khi biết chu vi và chiều dài

Đề bài: Cho một hình chữ nhật có chu vi là 36cm và chiều dài là 14cm. Hãy tìm chiều rộng của hình chữ nhật đó.

Bài giải:

Áp dụng công thức tính chu vi hình chữ nhật ta có:

P=(a+b)×2P=(a+b)\times 2
⇔b=(P÷2)−a\Leftrightarrow b=(P\div 2)- a
⇔b=(36÷2)−14\Leftrightarrow b=(36\div 2)-14
⇔b=4cm\Leftrightarrow b=4\,cm

Đáp số: Chiều rộng hình chữ nhật: 4 (cm)

Công thức tính chiều rộng hình chữ nhật khi biết nửa chu vi và chiều dài

Cách tính chiều rộng hình chữ nhật khi biết nửa chu vi và chiều dài ta lấy nửa chu vi trừ đi chiều dài.

Công thức:

b=C−ab=C-a

Trong đó:

  • C: Nửa chu vi hình chữ nhật thường có đơn vị thường là m, dm, cm,…
  • a: Chiều dài
  • b: Chiều rộng

Ví dụ cách tìm chiều rộng của hình chữ nhật khi biết nửa chu vi

Đề bài: Cho một hình chữ nhật có một nửa chu vi là 38cm và chiều dài là 26cm. Hãy tìm chiều rộng của hình chữ nhật đó.

Bài giải:

Áp dụng công thức tính nửa chu vi hình chữ nhật ta có:

C=a+bC=a+b
⇔b=C−a\Leftrightarrow b=C-a
⇔b=38−26\Leftrightarrow b=38-26
⇔b=12cm\Leftrightarrow b=12\,cm

Đáp số: Chiều rộng hình chữ nhật: 12 (cm)

Công thức tính chiều rộng hình chữ nhật khi biết diện tích và chiều dài

Cách tính chiều rộng hình chữ nhật khi biết diện tích và chiều dài ta lấy diện tích chia cho chiều dài.

Công thức:

b=S÷ab=S\div a

Trong đó:

  • S: Diện tích hình chữ nhật đơn vị tính thường là m2, dm2, cm2,…
  • a: Chiều dài
  • b: Chiều rộng

Ví dụ cách tìm chiều rộng của hình chữ nhật khi biết diện tích và chiều dài

Đề bài: Cho một hình chữ nhật biết diện tích là 120cm2 và chiều dài là 24cm. Hãy tìm chiều rộng của hình chữ nhật đó.

Bài giải:

Áp dụng công thức tính diện tích hình chữ nhật ta có:

S=a×bS=a\times b
⇔b=S÷a\Leftrightarrow b=S\div a
⇔b=120÷24\Leftrightarrow b=120\div 24
⇔b=5cm\Leftrightarrow b=5\,cm

Đáp số: Chiều rộng hình chữ nhật: 5 (cm)

Công thức tính chiều rộng hình chữ nhật khi chiều rộng kém chiều dài một số đo

Cách tính chiều rộng hình chữ nhật khi biết chiều rộng kém chiều dài một số đo c đơn vị ta lấy chiều dài trừ số đơn vị đo.

Công thức:

b=a−cb=a- c
  • a: Chiều dài
  • b: Chiều rộng
  • c: Số đơn vị đo chiều rộng kém chiều dài

Ví dụ cách tìm chiều rộng của hình chữ nhật khi chiều rộng kém chiều dài một số đo

Đề bài: Cho một hình chữ nhật chiều dài là 18cm, biết chiều rộng kém chiều dài 5cm. Hãy tìm chiều rộng của hình chữ nhật đó.

Bài giải:

Theo đề bài chiều rộng kém hơn chiều dài 5cm nên:

b=a−cb=a-c
⇔b=13−5\Leftrightarrow b=13-5
⇔b=8cm\Leftrightarrow b=8\,cm

Đáp số: Chiều rộng hình chữ nhật: 8 (cm)

Công thức tính chiều rộng hình chữ nhật khi biết đường chéo và chiều dài

Cách tính chiều rộng hình chữ nhật khi biết đường chéo và chiều dài ta lấy căn bậc 2 của bình phương đường chéo trừ đi bình phương chiều dài. Công thức này áp dụng dựa trên định lý Pythagore.

Công thức:

b=dc2−a2b=\sqrt{dc^{2}-a^{2} }

Trong đó:

  • a: Chiều dài
  • b: Chiều rộng
  • dc: Đường chéo

Ví dụ cách tìm chiều rộng của hình chữ nhật khi biết đường chéo và chiều dài

Đề bài: Cho một hình chữ nhật biết chiều dài là 8cm, biết đường chéo là 10cm . Hãy tìm chiều rộng của hình chữ nhật đó.

Bài giải:

Áp dụng định lý Pythagore ta có:

a=dc2−b2a=\sqrt{dc^{2}-b^{2} }
b=dc2−a2b=\sqrt{dc^{2}-a^{2} }
⇔b=102−82\Leftrightarrow b=\sqrt{10^{2}-8^{2} }
⇔b=100−64\Leftrightarrow b=\sqrt{100-64}
⇔b=64=6cm\Leftrightarrow b=\sqrt{64}=6\,cm

Đáp số: Chiều rộng hình chữ nhật: 6 (cm)

Công thức tính chiều rộng hình chữ nhật khi biết diện tích và chu vi

Cách tính chiều rộng hình chữ nhật khi biết diện tích và chu vi ta lấy chu vi chia cho 2 để được tổng chiều dài và chiều rộng. Dựa vào diện tích đã cho, tìm hai số có tổng bằng nửa chu vi và tích bằng diện tích. Trong hai số đó, số nhỏ hơn chính là chiều rộng hình chữ nhật.

Công thức:

{a+b=P2a×b=S \begin{cases} a + b = \frac{P}{2} \\ a \times b = S \end{cases}

Trong đó:

  • a: Chiều dài
  • b: Chiều rộng
  • P: Chu vi
  • S: Diện tích

Ví dụ cách tìm chiều rộng của hình chữ nhật khi biết diện tích và chu vi

Đề bài: Cho một hình chữ nhật biết diện tích là 80cm2 và chu vi là 36cm . Hãy tìm chiều rộng của hình chữ nhật đó.

Bài giải:

Dưa vào đề bài ta có hệ phương trình:

{a+b=P2a×b=S \begin{cases} a + b = \frac{P}{2} \\ a \times b = S \end{cases}
{a+b=362=18a×b=80\begin{cases} a + b = \frac{36}{2}=18 \\ a \times b = 80 \end{cases}
{b=18−aa×b=80\begin{cases} b=18-a\\ a \times b = 80 \end{cases}
{b=18−aa(18−a)=80\begin{cases} b=18-a\\ a (18-a) = 80 \end{cases}
{b=18−a18a−a2=80\begin{cases} b=18-a\\ 18a-a^{2} = 80 \end{cases}
{b=18−aa2−18a+80=0\begin{cases} b=18-a\\ a^{2} – 18a +80 = 0 \end{cases}

Giải phương trình bậc hai:

(a−10)(a−8)=0(a-10)(a-8)=0
a=10,a=8a=10\,,\,a=8

Vì chiều rộng bé hơn chiều dài nên: b = 8 cm, a = 10 cm

Các bài tập tự luyện tìm chiều rộng hình chữ nhật cho học sinh

Bài 1: Một hình chữ nhật có chu vi 28 cm, chiều dài 9 cm. Tính chiều rộng hình chữ nhật đó.

Bài 2: Chu vi của hình chữ nhật là 60 m, chiều dài 17 m. Tính chiều rộng của hình chữ nhật.

Bài 3: Nửa chu vi hình chữ nhật là 22 cm, chiều dài 13 cm. Tính chiều rộng hình chữ nhật.

Bài 4: Một hình chữ nhật có nửa chu vi 40 m, chiều dài 25 m. Tính chiều rộng hình chữ nhật.

Bài 5: Diện tích hình chữ nhật là 84 cm², chiều dài 12 cm. Tính chiều rộng hình chữ nhật.

Bài 6: Một mảnh đất hình chữ nhật có diện tích 240 m², chiều dài 30 m. Tính chiều rộng mảnh đất đó.

Bài 7: Chiều dài hình chữ nhật là 18 cm và kém chiều rộng 6 cm. Tính chiều rộng hình chữ nhật.

Bài 8: Chu vi hình chữ nhật là 48 cm, chiều dài gấp 3 lần chiều rộng. Tính chiều rộng hình chữ nhật.

Bài 9: Một hình chữ nhật có chu vi 50 cm và diện tích 150 cm². Tính chiều rộng hình chữ nhật.

Bài 10: Một hình chữ nhật có đường chéo 13 cm và chiều dài 12 cm. Tính chiều rộng hình chữ nhật.

Kết luận

Chiều rộng hình chữ nhật có thể được xác định bằng nhiều cách khác nhau, tùy theo các dữ kiện mà đề bài cho như chu vi, nửa chu vi, diện tích, đường chéo. Việc nắm vững từng công thức tính chiều rộng hình chữ nhật và hiểu rõ cách áp dụng sẽ giúp học sinh làm bài nhanh hơn, chính xác hơn và tránh được những sai lầm thường gặp. Thông qua các ví dụ minh họa và bài tập tự luyện mà Hoc2K đã chia sẻ hi vọng học sinh có thể rèn luyện kỹ năng giải toán hình học và củng cố kiến thức một cách hiệu quả.

User Rating: 5 (1 vote)

Tags:

Related Articles
Trang web học Online – Chia sẻ nội dung miễn phí dành cho người Việt
Trang học online - Soạn bài - Giải bài tập - Giải đề thi - Hoc2K.VN

Hoc2K - Nơi lan tỏa tri thức bằng cách tiếp cận sáng tạo và lôi cuốn. Đây không chỉ đơn thuần là một trang web học online trực tuyến, mà còn là một cộng đồng trực tuyến sôi động và năng lượng. Tại Hoc2K, bạn có thể tiếp cận kiến thức đa chiều và phong phú trong nhiều lĩnh vực khác nhau. Từ những kiến thức mới mẻ đến những chủ đề quen thuộc, tất cả đều được truyền tải một cách sinh động và cuốn hút, giúp mọi người dễ dàng tiếp thu và mở rộng tầm hiểu biết của mình.

DMCA.com Protection Status
Hỗ trợ thông tin
Liên hệ với chúng tôi
Web học online - Hoc2K
Logo