Trang chủ » Công thức Toán » Diện tích xung quanh hình hộp chữ nhật
Công thức Toán

Công thức tính diện tích xung quanh hình hộp chữ nhật: Hướng dẫn chi tiết và ví dụ

Tuấn Kiệt Tuấn Kiệt
23/12/2025
261 Views 0

Bạn đang tìm kiếm một hướng dẫn toàn diện, chính xác và dễ hiểu về công thức tính diện tích xung quanh hình hộp chữ nhật? Bài viết này từ Hoc2K sẽ mang đến cho bạn không chỉ công thức chuẩn xác, mà còn là giải thích cặn kẽ, ví dụ minh họa thực tế, các lưu ý quan trọng và ứng dụng vào đời sống học tập cũng như công việc.

Nội dung được xây dựng dựa trên nghiên cứu chuẩn xác từ sách giáo khoa Toán, tài liệu uy tín và kinh nghiệm giảng dạy thực tế được tổng hợp từ nhiều giáo viên. Phần giải thích ngắn gọn, dùng từ dễ hiểu, phù hợp cho cả học sinh tiểu học, phụ huynh và giáo viên.

Diện tích xung quanh hình hộp chữ nhật là gì?

Diện tích xung quanh hình hộp chữ nhật là phần diện tích của bốn mặt bên, không tính hai mặt đáy trên và dưới. Nói đơn giản, đó là “diện tích bề mặt xung quanh” của cái hộp.

Công thức tính diện tích xung quanh hình hộp chữ nhật

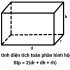
Cách tính diện tích xung quanh của hình hộp chữ nhật bằng 2 nhân với tổng chiều dài và chiều rộng mặt đáy rồi nhân với chiều cao. Hay nói cách khác là chu vi mặt đáy nhân với chiều cao

Cách tính diện tích xung quanh hình hộp chữ nhật:

Sxq=2×(d+r)×hS_{xq}=2\;\times\;(d\;+\;r)\;\times\;h

Hoặc

Sxq=Pđaˊy×hS_{xq}=P_{đáy}\times\;h

Trong đó:

  • Sxq: Diện tích xung quanh hình hộp chữ nhật (đơn vị thường dùng: cm², m²)
  • Pđáy: Chu vi mặt đáy
  • d: Chiều dài mặt đáy
  • r: Chiều rộng mặt đáy
  • h: Chiều cao

Công thức này là nền tảng để giải nhanh mọi bài toán liên quan đến tính diện tích xung quanh các khối hộp chữ nhật trong chương trình Toán tiểu học và Trung học cơ sở.

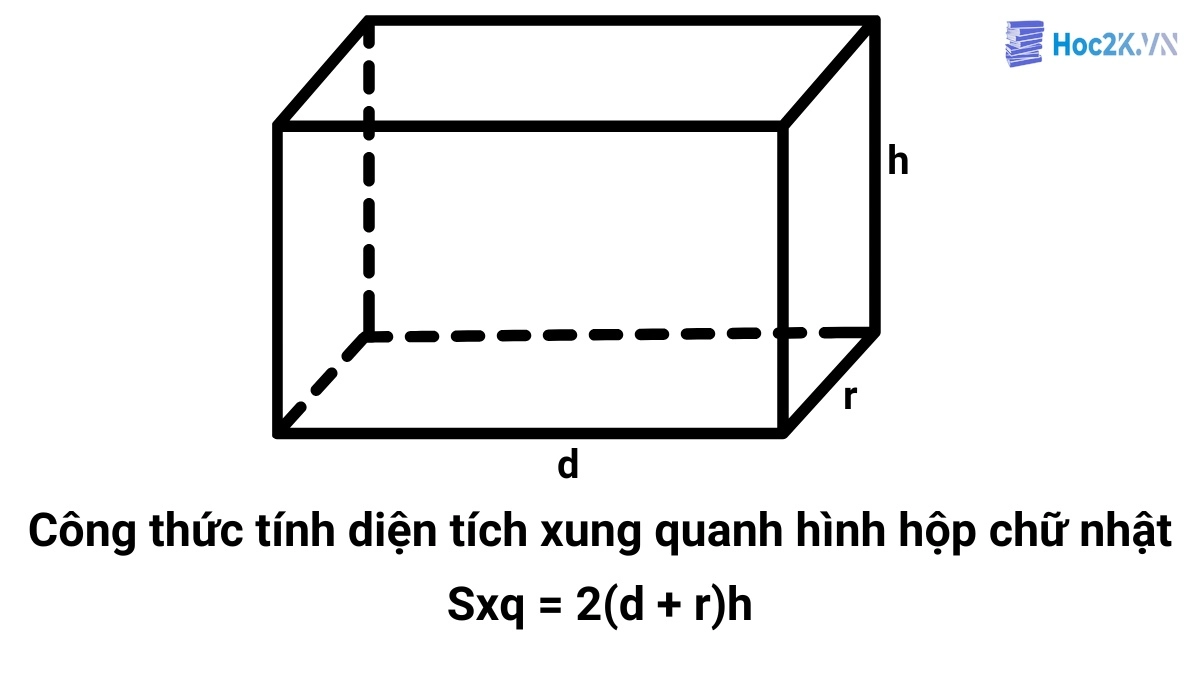
Công thức tính diện tích xung quanh hình hộp chữ nhật
Công thức tính diện tích xung quanh hình hộp chữ nhật

Hướng dẫn cách tính diện tích xung quanh hình hộp chữ nhật từng bước

Bước 1: Xác định chiều dài, chiều rộng, chiều cao

Để bắt đầu tính diện tích xung quanh hình hộp chữ nhật, bạn cần xác định ba kích thước quan trọng nhất của hình: chiều dài (d), chiều rộng (r) và chiều cao (h).

  • Chiều dài (d): Là cạnh dài hơn của đáy hình hộp.
  • Chiều rộng (r): Là cạnh còn lại của đáy vuông góc với chiều dài.
  • Chiều cao (h): Là khoảng cách thẳng đứng nối từ đáy lên nắp hộp.

Lưu ý: Bạn phải chắc chắn đã đo đúng và đủ ba kích thước này. Nếu đề bài cho các đại lượng bằng nhiều đơn vị khác nhau (cm, m, mm…), hãy thực hiện chuyển đổi về chung một đơn vị trước khi tính toán. Điều này giúp kết quả cuối cùng chính xác và dễ kiểm soát lỗi sai khi làm bài.

Bước 2: Tính chu vi mặt đáy

Chu vi mặt đáy (Pđáy) là tổng độ dài của bốn cạnh xung quanh mặt đáy hình hộp chữ nhật, và được xác định bằng công thức:

Pđaˊy=(d+r)×2{\mathrm P}_{\mathrm{đáy}}\;=\;(\mathrm d\;+\;\mathrm r)\;\times\;2

Bước 3: Nhân chu vi đáy với chiều cao

Sau khi đã có chu vi mặt đáy, bạn lấy giá trị này nhân với chiều cao (h) để tính diện tích xung quanh:

Sxq=Pđaˊy×h=2(d+r)×hS_{xq}=P_{đáy}\;\times\;h=\;2\;(d\;+\;r)\;\times\;h

Đây chính là diện tích của toàn bộ bốn mặt bên tượng trưng cho phần “vỏ ngoài” của hình hộp chữ nhật. Bước này giúp bạn hình dung: nếu “trải phẳng” lớp vỏ bốn mặt bên ra, chúng tạo thành một hình chữ nhật lớn với chiều dài bằng chu vi đáy và chiều rộng bằng chiều cao.

Bước 4: Kiểm tra đơn vị và kết quả

Bước cuối cùng nhưng vô cùng quan trọng là kiểm tra:

  • Đơn vị các kích thước có đồng nhất không? Nếu chưa, hãy đổi về chung một đơn vị (ưu tiên cm hoặc m tùy theo yêu cầu bài toán).
  • Kết quả diện tích xung quanh phải có đơn vị là đơn vị diện tích, ví dụ: cm², m².
  • Rà soát lại các bước tính toán: Đảm bảo quá trình cộng, nhân không có nhầm lẫn, đặc biệt với số thập phân hoặc chuyển đổi đơn vị.

Mẹo nhỏ: Hãy nhẩm lại quá trình, dùng máy tính hoặc nháp để thử lại một phép tính mẫu. Nếu cần, bạn có thể chuyển kết quả sang đơn vị lớn hơn/nhỏ hơn (ví dụ: 2,500cm² = 0,25m²) để tiện đối chiếu với thực tế hoặc đáp án.

Việc thực hiện đầy đủ bốn bước này không chỉ giúp bạn giải chính xác các bài toán hình học liên quan đến diện tích xung quanh hình hộp chữ nhật, mà còn nâng cao kỹ năng tư duy logic, kiểm soát quy trình giải toán và áp dụng vào thực tiễn một cách hiệu quả từ học tập đến đời sống sản xuất và thiết kế.

Ví dụ minh họa chi tiết có lời giải

Dưới đây là những ví dụ thực tiễn bám sát chương trình học, kèm phân tích chi tiết từng bước, giúp bạn hiểu sâu và tự tin áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật vào các tình huống khác nhau. Tất cả ví dụ đều được kiểm chứng về độ chính xác, có hướng dẫn chuyển đổi đơn vị và nhận xét kết quả.

Ví dụ 1: Bài toán cơ bản với số nguyên

Đề bài: Một hình hộp chữ nhật có chiều dài d = 6cm, chiều rộng r = 4cm, chiều cao h = 10cm. Tính diện tích xung quanh hình hộp này.

Lời giải:

Bước 1: Tính chu vi mặt đáy

Pđaˊy=2(a+b)=2(6+4)=2×10=20cmP_{đáy}=\;2(a+b)\;=\;2(6+4)\;=\;2\;\times\;10=\;20\;cm

Bước 2: Nhân chu vi với chiều cao

Sxq=Pđaˊy×h=20×10=200cm2S_{xq}=P_{đáy}\;\times\;h=20\;\times\;10\;=\;200\;cm^2

Đáp số: Diện tích xung quanh là 200 cm².

Ví dụ 2: Bài toán với số thập phân

Đề bài: Một bể cá hình hộp chữ nhật có chiều dài d = 12.5 dm, chiều rộng r = 5.2 dm , chiều cao h = 4.5 dm. Hỏi diện tích xung quanh bể cá là bao nhiêu dm2?

Lời giải:

Bước 1: Chu vi mặt đáy:

Pđaˊy=2(d+br=2(12.5+5.2)=2×17.7=35.4dmP_{đáy}=\;2(d+br\;=\;2(12.5+5.2)\;=\;2\;\times\;17.7\;=\;35.4\;dm

Bước 2: Nhân chu vi với chiều cao:

Sxq=35.4×4.5=159.3dm2S_{xq}=\;35.4\;\times\;4.5\;=\;159.3\;dm^2

Đáp số: Diện tích xung quanh bể cá là 159.3 dm2

Ví dụ 3: Bài toán ứng dụng thực tế

Đề bài: Một thùng giấy hình hộp chữ nhật dùng để đóng gói hàng, có chiều dài d = 40 cm, chiều rộng r = 25 cm và chiều cao h = 30 cm. Tính diện tích giấy cần thiết để dán kín 4 mặt bên thùng (không tính nắp và đáy).

Ví dụ 4: Tìm chiều cao khi biết diện tích xung quanh

Lời giải:

Bước 1: Chu vi đáy

Pđaˊy=2(d+r)=2(40+25)=2×65=130cmP_{đáy}=2(d+r)\;=\;2(40\;+\;25)\;=\;2\;\times\;65=130\;cm

Bước 2: Tính diện tích xung quanh

Sxq=Pđaˊy×h=130×30=3,900cm2S_{xq}=P_{đáy}\;\times\;h\;=\;130\;\times\;30\;=\;3,900\;cm^2

Đổi ra m2: 3,900 cm2 = 0,39 m2

Nhận xét: Khi in hoặc cắt giấy, nên cộng thêm phần mép dán (vài cm).

Đáp số: Cần 3,900cm² (0,39m²) giấy để dán quanh thân thùng.

Các dạng bài tập thường gặp và phương pháp giải

Để giúp bạn làm chủ mọi dạng toán về diện tích xung quanh hình hộp chữ nhật, dưới đây là tổng hợp các dạng bài tập thường gặp nhất, phân tích phương pháp giải tương ứng và minh họa ngắn gọn cho từng loại.

Dạng 1: Tính diện tích xung quanh khi biết đủ thông số

Đặc điểm: Đề bài cho trực tiếp hoặc gián tiếp đầy đủ các kích thước của hình hộp chữ nhật: chiều dài (d), chiều rộng (r), chiều cao (h).

Phương pháp giải:

Xác định ba kích thước d, r, h

Áp dụng công thức

Sxq=2×h×(d+r)S_{xq}=\;2\times h\times (d+r)

hoặc các biến thể tương đương.

Kiểm tra và đồng nhất đơn vị trước khi tính.

Đưa ra đáp số có đơn vị diện tích phù hợp.

Ví dụ:

Một thùng gỗ hình hộp chữ nhật: d =15 cm, r = 10 cm, h = 7cm.

Sxq=2×7×(15+10)=2×7×25=350cm2S_{xq}=2\;\times\;7\;\times\;(15+10)\;=\;2\times7\times25\;=\;350\;cm^2

Đáp số: 350 cm2

Dạng 2: Tìm thông số chưa biết

Đặc điểm: Bài toán cho biết diện tích xung quanh và hai trong ba kích thước, yêu cầu tìm đại lượng còn lại (d, r hoặc h).

Phương pháp giải:

Áp dụng công thức đảo ngược:

h=Sxq2(d+r)h=\frac{S_{xq}}{2(d+r)}

hoặc

d=Sxq2h−rd=\frac{S_{xq}}{2h}-r

hoặc

r=Sxq2h−dr=\frac{S_{xq}}{2h}-d

Xác định và chuyển đổi đơn vị hợp lý sau đó diễn giải quá trình đảo công thức một cách rõ ràng.

Ứng dụng thực tế của diện tích xung quanh hình hộp chữ nhật

Tính lượng sơn cần thiết cho thùng container

Khi muốn sơn phủ bề mặt bên ngoài của một thùng container hình hộp chữ nhật, việc xác định chuẩn diện tích xung quanh là bước bắt buộc để tính chính xác lượng sơn cần mua.

Giả sử bạn đang chuẩn bị bảo trì hoặc làm mới container, hãy làm theo các bước sau:

  • Đo chiều dài, chiều rộng, chiều cao của container (ví dụ: dài 12m, rộng 2.5m, cao 2.9m).
  • Áp dụng công thức

        \[S_{xq}=2h(d+r)\]

    , với d là chiều dài, r là chiều rộng, h là chiều cao.
  • Kết quả cho biết tổng diện tích bốn mặt bên tức lượng bề mặt bạn cần sơn.
  • Tiếp theo, dựa vào tem hoặc chỉ dẫn của hãng sơn (ví dụ: 1 lít sơn phủ được 10m² bề mặt), bạn chia diện tích vừa tính cho độ phủ mỗi lít để biết cần bao nhiêu lít sơn.

Mẹo thực tế: Nên cộng thêm 5–10% cho sai số thi công hoặc bề mặt không đều để tránh thiếu vật liệu.

Ước tính vật liệu xây dựng

Trong lĩnh vực xây dựng, việc tính toán diện tích xung quanh hình hộp chữ nhật cực kỳ hữu ích để:

  • Ước lượng số lượng gạch, tấm ốp, giấy dán tường cần dùng cho các phòng, kho, nhà kho (có dạng hộp chữ nhật).
  • Xác định số mét vuông tường cần xây, sơn hoặc bọc cách nhiệt cho các khối nhà đơn giản.
  • Dự tính lượng vật tư như bạt che, lưới bảo vệ khi che phủ nhà xưởng, container, khu vực lưu trữ ngoài trời.

Ví dụ thực tiễn: Khi xây dựng một phòng kho kích thước d = 6 m , r = 4 m, h = 3.2 m, sử dụng công thức diện tích xung quanh giúp bạn tính ra tổng diện tích để mua số lượng gạch, xi măng, bạt hoặc giấy dán phù hợp mà không bị dư thừa hoặc thiếu hụt.

Thiết kế nội thất và trang trí

Công thức này xuất hiện trong các hoạt động thiết kế nội thất, trang trí nhà cửa, trường học, văn phòng:

  • Tính diện tích dán decal, ốp đá, giấy dán tường quanh các khối tủ, quầy bar, hộp chứa vật dụng, tường phòng (khi đóng trần sàn kín, tường các mặt).
  • Xác định diện tích cần làm cách âm, chống nóng cho các phòng thu, phòng học, phòng ngủ dạng hộp chữ nhật.
  • Ước lượng lượng vải bọc cho vật thể trang trí có dạng hình hộp chữ nhật như bọc quà, hộp trưng bày, tủ gỗ.

Thực tế, các kiến trúc sư, kỹ sư thiết kế lập dự toán vật tư đều xuất phát từ số đo bề mặt các mặt bên của “hộp” nội thất dựa trên công thức diện tích xung quanh.

Các nghề nghiệp sử dụng công thức này

Công thức diện tích xung quanh hình hộp chữ nhật là công cụ thường xuyên được vận dụng trong nhiều ngành nghề, bao gồm:

  • Xây dựng và thiết kế kiến trúc: Kỹ sư, kiến trúc sư, nhà thầu, thợ xây.
  • Sản xuất bao bì, đóng gói hàng hóa: Thiết kế, cắt dán, đóng hộp.
  • Nhân viên logistics, kho vận: Tối ưu hóa diện tích bề mặt khi lưu trữ, vận chuyển vật phẩm dạng hộp.
  • Nghề mộc, nội thất: Sản xuất tủ, kệ, hộp gỗ, máng, hộp kỹ thuật.
  • Dạy học và giáo dục: Giáo viên, gia sư hướng dẫn thực hành toán ứng dụng.
  • Ngành trang trí, quảng cáo: Thi công bảng hiệu, bọc hộp đèn, thủ công mỹ nghệ hộp quà tặng.

Kinh nghiệm chia sẻ: Trong thực tiễn, mọi lĩnh vực liên quan đến “vật thể hình hộp” đều cần nắm chắc công thức này để tiết kiệm vật tư, kiểm soát chi phí và đảm bảo độ chính xác kỹ thuật trong công việc cũng như đời sống hằng ngày.

Bài tập thực hành tự luyện

Việc luyện tập thường xuyên với các dạng bài đa dạng là cách tốt nhất để củng cố lý thuyết, nâng cao kỹ năng và tự đánh giá mức độ thành thạo về công thức tính diện tích xung quanh hình hộp chữ nhật. Dưới đây là các bài tập các em học sinh có thể tự luyện tập.

10 Bài tập cơ bản có đáp án

Một hình hộp chữ nhật có chiều dài 8 cm, chiều rộng 5 cm, chiều cao 6 cm. Tính diện tích xung quanh.

Đáp án:

Sxq=2×6×(8+5)=156cm2S_{xq}=2\times6\times(8+5)=156\;cm^2

Hình hộp chữ nhật với d = 10 cm, r = 4 cm, h = 12 cm. Tìm diện tích xung quanh.

Đáp án:

2×12×(10+4)=336cm22\times12\times(10+4)=336\;cm^2

Tính diện tích xung quanh của hình hộp chữ nhật có d = 7 dm, r =3 dm , h = 4 dm.

Đáp án:

2×4×(7+3)=80dm22\times4\times(7+3)=80\;dm^2

Chiều dài d = 0,8 m, chiều rộng r = 0,6 m, chiều cao h = 1,2 m. Sxq bằng bao nhiêu?

Đáp án:

2×1,2×(0,8+0,6)=2,88m22\times1,2\times(0,8+0,6)=2,88\;m^2

d = 25cm, r = 17 cm, h = 9 cm. Hỏi diện tích xung quanh.

Đáp án:

2×9×(25+17)=2×9×42=756cm22\times9\times(25+17)=2\times9\times42=756\;cm^2

Một thùng giấy: d = 15 cm, r = 20 cm, h = 30 cm. Tìm Sxq.

Đáp án:

2×30×(15+20)=2×30×35=2,100cm22\times30\times(15+20)=2\times30\times35=2,100\;cm^2

Hình hộp chữ nhật: d = 6 cm, r = 5 cm, h = 9 cm. Diện tích xung quanh là?

Đáp án:

2×9×(6+5)=2×9×11=198cm22\times9\times(6+5)=2\times9\times11=198\;cm^2

Nếu d = 12 dm, r = 7 dm, h = 8 dm. Sxq bằng?

Đáp án:

2×8×(12+7)=2×8×19=304dm22\times8\times(12+7)=2\times8\times19=304\;dm^2

Hình hộp có d = 9 cm, r = 4 cm, h = 10 cm. Diện tích xung quanh là:

Đáp án:

2×10×(9+4)=2×10×13=260cm22\times10\times(9+4)=2\times10\times13=260\;cm^2

Một hộp quà: d = 13 cm, r = 9 cm, h = 6 cm. Tìm diện tích xung quanh.

Đáp án:

2×6×(13+9)=2×6×22=264cm22\times6\times(13+9)=2\times6\times22=264\;cm^2

5 Bài tập nâng cao

Hình hộp chữ nhật có diện tích xung quanh Sxq = 220 cm2, chiều dài d = 10 cm, chiều rộng r = 6 cm. Tìm chiều cao h.

Đáp án:

h=2202×(10+6)=22032=6.875cmh=\frac{220}{2\times(10+6)}=\frac{220}{32}=6.875\;cm

Một bể cá có chiều cao là 12 cm, diện tích xung quanh là 480 cm2, chiều dài hơn chiều rộng 4 cm, chiều dài là d, chiều rộng là r. Biết d + r = x. Tìm d, r.

Hướng dẫn: Đặt d = r + 4, 2h(d + r) = 480; 2 x 12 x (r + 4 +r) = 480

Hình hộp chữ nhật có diện tích xung quanh gấp đôi diện tích đáy. Biết d = 8 cm, r = 7 cm, tìm h.

Đáp án:

Sxq=2Sđaˊy→2h(d+r)=2dr→h(d+r)=dr→h=drd+r=8×715=5615≈3.73cmS_{xq}=2S_{đáy}\rightarrow2h(d+r)=2dr\rightarrow h(d+r)=dr\rightarrow h=\frac{dr}{d+\;r}=\frac{8\times7}{15}=\frac{56}{15}\approx3.73\;cm

Một khối hộp có d, r, h đều là số nguyên, d + r = 17 cm, h = 6 cm, diện tích xung quanh là Sxq = 204 cm2. Tìm d, r.

Đáp án:

Sxq=2h(d+r)=2×6×17=204cm2S_{xq}=2h(d+r)=2\times6\times17=204\;cm^2

thỏa mãn mọi giá trị d, r nguyên d + r = 17.

Hộp carton có chiều dài gấp 3 lần chiều rộng, chiều cao bằng chiều rộng, diện tích xung quanh là 480 cm2. Tìm kích thước các cạnh.

Gọi r là x, d = 3x, h = x

Đáp án:

Sxq=2h(d+r)=2x(3x+x)=2x(3x+x)=2x×4x=8x2=480⇒x≈60≈7.75cmS_{xq}=2h(d+r)\;=\;2x(3x+x)\;=2x(3x+x)\;=2x\times4x\;=8x^2=480\;\Rightarrow x\approx\sqrt{60}\approx7.75\mathrm{cm}
a≈3x=3×7.75≈x=7.75cma \approx 3x= 3\times 7.75\approx x= 7.75cm

Bài tập ứng dụng thực tế

Tính diện tích decal cần dán bốn mặt bên ngoài của một bể cá có kích thước d = 80 cm, r = 40 cm, h = 50cm.

Đáp án:

2×50×(80+40)=2×50×120=12,000cm2=1.2m22\times50\times(80+40)=2\times50\times120=12,000\;cm^2=1.2\;m^2

Một kho chứa có kích thước d =12 m, r = 5 m, h = 3 m. Tính diện tích sơn cần sơn bốn vách tường.

Đáp án:

2×3×(12+5)=2×3×17=102m22\times3\times(12+5)=2\times3\times17=102\;m^2

Một thùng tôn đặc có chiều dài 3 m, chiều rộng 1.2 m, cao 0.7 m. Tính diện tích cần dùng để làm 4 mặt bên ngoài.

Đáp án:

2×0.7×(3+1.2)=2×0.7×4.2=5.88m22\times0.7\times(3+1.2)=2\times0.7\times4.2=5.88\;m^2

Một phòng học hình hộp chữ nhật không có cửa sổ, dài 8 m, rộng 6 m, cao 3.4 m. Muốn dán giấy quanh bốn bức tường, cần bao nhiêu m² giấy?

Đáp án:

2×3.4×(8+6)=2×3.4×14=95.2m22\times3.4\times(8+6)=2\times3.4\times14=95.2\;m^2

Công ty muốn sản xuất bìa nhựa bọc ngoài thùng carton (d = 0.5 m,b = 0.35 m, h = 0.6 m). Tính diện tích nhựa cần dùng.

Đáp án:

2×0.6×(0.5+0.35)=2×0.6×0.85=1.02m22\times0.6\times(0.5+0.35)=2\times0.6\times0.85=1.02\;m^2

Kết luận

Trên đây là công thức và các dạng bài tập về diện tích xung quanh hình hộp chữ nhật, giúp học sinh nắm chắc kiến thức cơ bản và áp dụng linh hoạt vào giải toán cách tính diện tích xung quanh hình hộp chữ nhật. Hy vọng qua bài viết này Hoc2K đã có thể giúp các bạn có thể tự tin hơn khi gặp các bài toán liên quan và tiếp tục rèn luyện để nâng cao kỹ năng. Chúc các bạn học tốt!

User Rating: 5 (1 vote)

Tags:

Related Articles
Trang web học Online – Chia sẻ nội dung miễn phí dành cho người Việt
Trang học online - Soạn bài - Giải bài tập - Giải đề thi - Hoc2K.VN

Hoc2K - Nơi lan tỏa tri thức bằng cách tiếp cận sáng tạo và lôi cuốn. Đây không chỉ đơn thuần là một trang web học online trực tuyến, mà còn là một cộng đồng trực tuyến sôi động và năng lượng. Tại Hoc2K, bạn có thể tiếp cận kiến thức đa chiều và phong phú trong nhiều lĩnh vực khác nhau. Từ những kiến thức mới mẻ đến những chủ đề quen thuộc, tất cả đều được truyền tải một cách sinh động và cuốn hút, giúp mọi người dễ dàng tiếp thu và mở rộng tầm hiểu biết của mình.

DMCA.com Protection Status
Hỗ trợ thông tin
Liên hệ với chúng tôi
Web học online - Hoc2K
Logo