Công thức tính diện tích toàn phần hình hộp chữ nhật là kiến thức toán lớp 5 giúp các em dễ dàng tính toán bề mặt các vật dụng hàng ngày như hộp quà, tủ quần áo hay bể nước. Hoc2K sẽ giúp các bạn cách tính diện tích toàn phần hình hộp chữ nhật đơn giản, dễ hiểu dễ hiểu nhất kèm các ví dụ minh họa từ cơ bản đến nâng cao.
Diện tích toàn phần hình hộp chữ nhật là gì?
Diện tích toàn phần hình hộp chữ nhật là tổng diện tích của tất cả 6 mặt bao quanh hình khối, giống như “bộ quần áo hoàn chỉnh” phủ kín cả bên trong lẫn bên ngoài cái hộp.
Công thức tính diện tích toàn phần hình hộp chữ nhật
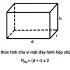
Cách tính diện tích toàn phần hình hộp chữ nhật bằng tổng diện tích xung quanh cộng với diện tích hai mặt đáy. Khác với diện tích xung quanh hình hộp chữ nhật chỉ tính 4 mặt bên, diện tích toàn phần cộng thêm cả 2 mặt đáy để có tổng bề mặt hoàn chỉnh.
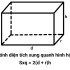
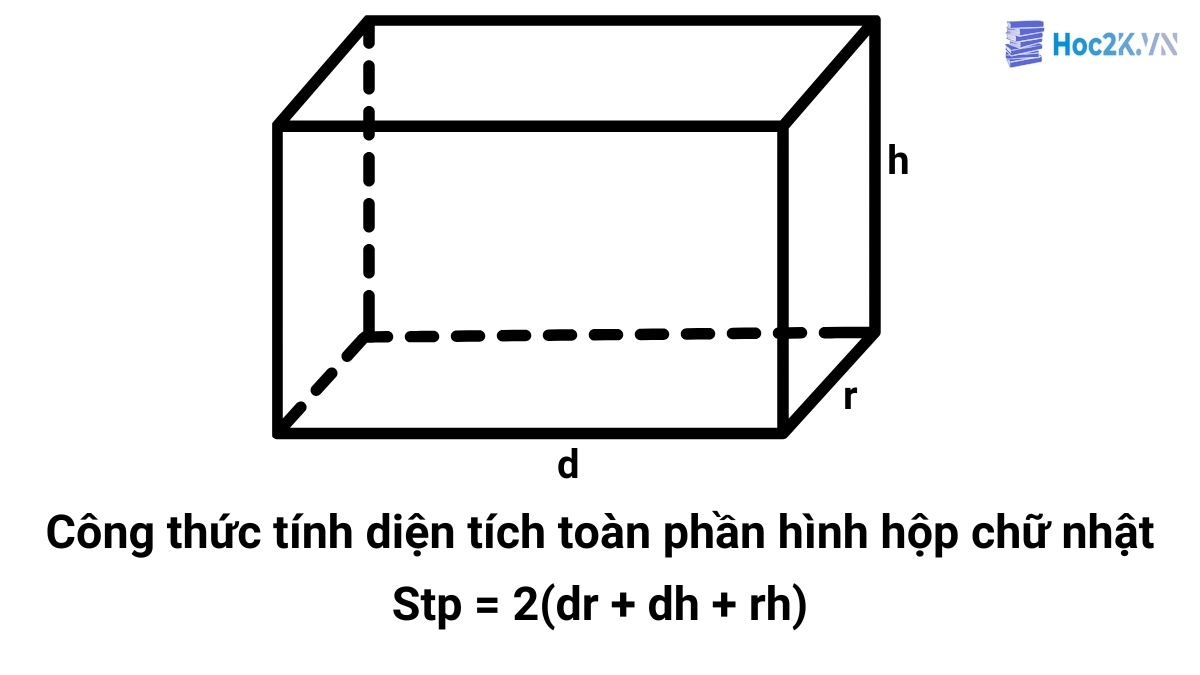
Cách tính diện tích toàn phần hình hộp chữ nhật:
hoặc có thể diễn đạt bằng một công thức khác là diện tích hình hộp chữ nhật bằng gấp đôi chiều cao nhân với tổng chiều dài cộng chiều rộng.
Trong đó:
Stp: Diện tích toàn phần hình hộp chữ nhật
d: Chiều dài mặt đáy
r: Chiều rộng mặt đáy
h: Chiều cao
Đơn vị tính diện tích toàn phần hình hộp chữ nhật
Đơn vị diện tích toàn phần hình hộp chữ nhật có sẽ phụ thuộc vào đơn vị của các chiều. Nếu chiều dài, chiều rộng và chiều cao được đo bằng mét (m), thì diện tích toàn phần sẽ có đơn vị là mét (m2). Nếu các chiều được đo bằng centimet (cm), thì diện tích toàn phần sẽ có đơn vị là centimet (cm2).
Ví dụ áp dụng công thức tính diện tích toàn phần hình hộp chữ nhật
Ví dụ: Cho hình hộp chữ nhật có chiều dài là 10 cm, chiều rộng là 5 cm, chiều cao là 7 cm. Hãy tính diện tích toàn phần của hình hộp chữ nhật
Bài giải:
Diện tích toàn phần hình hộp chữ nhật là: Stp= 2 (10 x 5 + 10 x 7 + 5 x 7) = 310 (cm2)
Đáp số: 310 (cm2)
Các dạng toán tính diện tích toàn phần hình hộp chữ nhật thường gặp
Trong toán học, các bài tập tính diện tích toàn phần của hình hộp chữ nhật thường xoay quanh các dạng bài khác nhau tùy thuộc vào cách đề bài đưa ra thông tin. Dưới đây là một số dạng bài tập phổ biến để các bạn học sinh hiểu rõ hơn cách tính diện tích toàn phần hình hộp chữ nhật:
Tính diện tích toàn phần hộp chữ nhật khi biết chiều dài, chiều rộng và chiều cao
Ví dụ: Tính diện tích toàn phần của hình hộp chữ nhật biết chiều dài 8 cm, chiều rộng 6 cm và chiều cao 7 cm
Bài giải:
Áp dụng công thức tính diện tích toàn phần hộp chữ nhật ta có: Stp = 2 x (8 x 6 + 8 x 7 + 6 x 7) = 292 (cm2)
Đáp số:
Diện tích toàn phần hộp chữ nhật: 292 (cm2)
Tính diện tích toàn phần hình hộp chữ nhật khi biết thể tích
Ví dụ: Hình hộp chữ nhật có thể tích V = 120 cm3 . Chiều dài d = 10 cm, chiều rộng r = 4 cm. Tính diện tích toàn phần của hình hộp chữ nhật đó.
Bài giải:
Áp dụng công thức thể tích hình hộp chữ nhật để tìm chiều cao: V = d x r x h
120 = 10 x 4 x h
h = 3 (cm)
Áp dụng công thức tính diện tích toàn phần hình hộp chữ nhật ta có: Stp = 2 x (d x r + d x h + r x h) = 2 x ( 10 x 4 + 10 x 3 + 4 x 3) = 164 (cm2)
Đáp số:
Diện tích toàn phần hình hộp chữ nhật: 84 (cm2)
Kết luận
Trên đây là công thức và các dạng bài tập về công thức tính diện tích toàn phần của hình hộp chữ nhật, giúp học sinh nắm chắc kiến thức cơ bản và áp dụng linh hoạt vào giải toán cách tính diện tích toàn phần của hình hộp chữ nhật. Hy vọng qua bài viết này Hoc2K đã có thể giúp các bạn có thể tự tin hơn khi gặp các bài toán liên quan và tiếp tục rèn luyện để nâng cao kỹ năng. Chúc các bạn học tốt!
